题目内容
已知函数![]() 是定义在
是定义在![]() 上的奇函数,其值域为
上的奇函数,其值域为![]() .
.
(Ⅰ)试求![]() 的值.
的值.
(Ⅱ)函数![]() 满足:①当
满足:①当![]() 时,
时,![]() ;②
;②![]() .
.
①求函数![]() 在
在![]() 上的解析式.
上的解析式.
②若函数![]() 在
在![]() 上的值域是闭区间,试探求
上的值域是闭区间,试探求![]() 的取值范围,并说明理由.
的取值范围,并说明理由.
解:(Ⅰ)![]() 定义域为
定义域为![]() ,
,![]() .
.
又![]() 为奇函数,由
为奇函数,由![]() 对
对![]() 恒成立,得
恒成立,得![]() ……………………………………2分
……………………………………2分
因为![]() 的定义域为R,所以方程
的定义域为R,所以方程![]() 在R上有解,
在R上有解,
当![]() 时,由
时,由![]() ,得
,得![]() ,而
,而![]() 的值域为
的值域为![]() ,所以
,所以![]() ,解得
,解得![]() ;
;
当![]() 时,得
时,得![]() ,可知
,可知![]() 符合题意.所以
符合题意.所以![]() ……………………………………………………5分
……………………………………………………5分
(Ⅱ)①因为当![]() 时,
时, ![]() ,所以
,所以
当![]() 时,
时,![]() ……………………………………………………6分
……………………………………………………6分
当![]() 时,
时,![]() ,
,
 ……………………………………………………………………9分
……………………………………………………………………9分
②因为当![]() 时,
时,![]() 在
在![]() 处取得最大值为
处取得最大值为![]() ,在
,在![]() 处取得最小值为0……10分
处取得最小值为0……10分
所以当![]() ,
,![]() 分别在
分别在![]() 和
和![]() 处取得最值为
处取得最值为![]() 与0……………………………………………………………………………………………11分
与0……………………………………………………………………………………………11分
(1)当![]() 时,
时,![]() 的值趋向无穷大,从而
的值趋向无穷大,从而![]() 的值域不为闭区间…………12分
的值域不为闭区间…………12分
(2)当![]() 时,由
时,由![]() 得
得![]() 是
是![]() 为周期的函数,从而
为周期的函数,从而![]() 的值域为闭区间
的值域为闭区间![]() 13分
13分
(3)当![]() 时,由
时,由![]() 得
得![]() ,得
,得![]() 是
是![]() 为周期的函数,
为周期的函数,
且当![]()
![]() 值域为
值域为![]() ,从而
,从而![]() 的值域为闭区间
的值域为闭区间![]() ………14分
………14分
(4)当![]() 时,由
时,由![]() ,得
,得![]() 的值域为闭区间
的值域为闭区间![]() ………………15分
………………15分
(5)当![]() 时,由
时,由![]() ,从而
,从而![]() 的值域为闭区间
的值域为闭区间![]() ,
,
综上知,当![]() ,即
,即![]() 或
或![]() 时,
时,![]() 的值域为闭区间…………16分
的值域为闭区间…………16分

练习册系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。 的解析式;
的解析式; 。
。 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式;
 是定义在
是定义在 上的以5为周期的奇函数, 若
上的以5为周期的奇函数, 若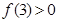 ,
, ,则a的取值范围是 ( )
,则a的取值范围是 ( )  B.
B.

 D.
D.

 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
) ,求证:当
,求证:当 时,
时, ;
; 时,
时, 是定义在
是定义在 上的奇函数,且
上的奇函数,且
 的解析式;
的解析式; 的单调性;
的单调性;