题目内容
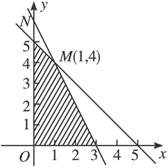
如图,阴影部分的点满足不等式组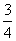 在这些点中,使目标函数k=6x+8y取得最大值的点的坐标是___________________.
在这些点中,使目标函数k=6x+8y取得最大值的点的坐标是___________________. 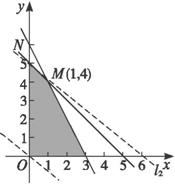
思路解析:可以利用函数的单调性求最值,也可以利用截距法或平移法.
解法一:由图可知,使目标函数k=6x+8y取得最大值的点一定在边界x+y=5或2x+y=6上取得.
①当0≤x≤1时,k=6x+8y=6x+8(5-x)=40-2x,在[0,1]上为减函数,所以当x=0时,kmax=40.
②当1≤x≤3时,k=6x+8y=6x+8(6-2x)=48-10x,在[1,3]上也是减函数,所以当x=1时,kmax=38.
由①②知,当x=0时,k=6x+8y的取值最大,此时y=5,所以所求点的坐标为(0,5).
解法二:要使目标函数k=6x+8y取得最大值,即使直线y=-![]() x+
x+![]() 的截距最大,且阴影部分的点至少有一个在直线y=-
的截距最大,且阴影部分的点至少有一个在直线y=-![]() x+
x+![]() 上,因为-
上,因为-![]() >-1>-2,所以易知所求点的坐标为(0,5).
>-1>-2,所以易知所求点的坐标为(0,5).

解法三:如上图,作直线l:6x+8y=0,即作直线l:3x+4y=0.把直线l向右上方平移至l2的位置,即直线l2过可行域上的N点时,k=6x+8y取最大值.
解方程组![]() 得
得![]() 即N点坐标为(0,5),代入目标函数k=6x+8y,得k=6×0+8×5=40.故知所求点为(0,5)时,k=6x+8y取最大值40.
即N点坐标为(0,5),代入目标函数k=6x+8y,得k=6×0+8×5=40.故知所求点为(0,5)时,k=6x+8y取最大值40.

练习册系列答案
相关题目
 为了测算如图阴影部分的面积,做一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点.已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是
为了测算如图阴影部分的面积,做一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点.已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是 为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( )
为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( ) (2000•上海)图中阴影部分的点满足不等式组
(2000•上海)图中阴影部分的点满足不等式组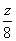 在这些点中,求使z=6x+8y取得最大值的点的坐标.
在这些点中,求使z=6x+8y取得最大值的点的坐标.