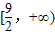题目内容
已知a，b均为正数，
+
=2，则a+b的取值范围是（ ）
| 1 |
| a |
| 4 |
| b |
A、[
| ||
| B、[1，+∞） | ||
| C、[9，+∞） | ||
| D、[8，+∞） |
分析：由题知 a+b=
(a+b)(
+
) =
+
+
+2≥
+2
=
．由此可知答案．
| 1 |
| 2 |
| 1 |
| a |
| 4 |
| b |
| 1 |
| 2 |
| b |
| 2a |
| 2a |
| b |
| 5 |
| 2 |
|
| 9 |
| 2 |
解答：解：∵a，b均为正数，
+
=2，
∴a+b=
(a+b)(
+
) =
+
+
+2
≥
+2
=
．
则a+b的取值范围是[
，+∞)
故选A．
| 1 |
| a |
| 4 |
| b |
∴a+b=
| 1 |
| 2 |
| 1 |
| a |
| 4 |
| b |
| 1 |
| 2 |
| b |
| 2a |
| 2a |
| b |
≥
| 5 |
| 2 |
|
| 9 |
| 2 |
则a+b的取值范围是[
| 9 |
| 2 |
故选A．
点评：本题考查了基本不等式在最值问题中的应用，考查了均值不等式，灵活运用了“2”的代换，是高考考查的重点内容．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
+
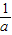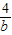=2，则a+b的取值范围是（ ）