题目内容
已知a，b均为正数且acos2θ+bsin2θ≤6，则
cos2θ+
sin2θ的最大值为
．
| a |
| b |
| 6 |
| 6 |
分析：由柯西不等式可得：（acos2θ+bsin2θ）（cos2θ+sin2θ）≥（
cos2θ+
sin2θ）2，再由已知易求．
| a |
| b |
解答：解：由柯西不等式可得：（acos2θ+bsin2θ）（cos2θ+sin2θ）≥（
cos2θ+
sin2θ）2的
∴
cos2θ+
sin2θ≤
≤
故答案为：
| a |
| b |
∴
| a |
| b |
| acos2θ+bsin2θ |
| 6 |
故答案为：
| 6 |
点评：本题考查柯西不等式的简单应用，属于基础题．
练习册系列答案
相关题目
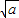cos2θ+
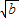sin2θ的最大值为 ．
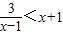的解集为{x|x＜-2，或x＞2}；
，则a+b的最小值为9；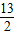
；
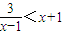的解集为{x|x＜-2，或x＞2}；
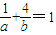，则a+b的最小值为9；
；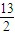