题目内容
设OABC是四面体,G1是△ABC的重心,G是OG1上一点,且OG=3GG1,若
=x
+y
+z
,则(x,y,z)为( )
| OG |
| OA |
| OB |
| OC |
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(
|
分析:由题意推出
,使得它用
,
,
,来表示,从而求出x,y,z的值,得到正确选项.
| OG |
| OA |
| OB |
| OC |
解答:解:∵
=
=
(
+
)
=
+
•
[
(
+
)]=
+
[(
-
)+(
-
)]
=
+
+
,
而
=x
+y
+z
,∴x=
,y=
,z=
.
故选A.
| OG |
| 3 |
| 4 |
| OG1 |
| 3 |
| 4 |
| OA |
| AG1 |
=
| 3 |
| 4 |
| OA |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| AB |
| AC |
| 3 |
| 4 |
| OA |
| 1 |
| 4 |
| OB |
| OA |
| OC |
| OA |
=
| 1 |
| 4 |
| OA |
| 1 |
| 4 |
| OB |
| 1 |
| 4 |
| OC |
而
| OG |
| OA |
| OB |
| OC |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
故选A.
点评:本题考查空间向量的加减法,考查待定系数法,是基础题.

练习册系列答案
相关题目
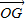 =x
=x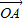 +y
+y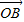 +z
+z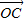 ,则(x,y,z)为( )
,则(x,y,z)为( ) ,
, ,
, )
) ,
, ,
, )
) ,
, ,
, )
) ,
, ,
, )
) =x
=x +y
+y +z
+z ,则(x,y,z)为 .
,则(x,y,z)为 .