题目内容
从某大学中随机选取8名女大学，其身高与体重的数据如下：
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 身高（cm） | 165 | 165 | 157 | 170 | 175 | 165 | 155 | 170 |
| 体重（kg） | 48 | 57 | 50 | 54 | 64 | 61 | 43 | 59 |
（1）不画散点图判断体重与身高是否具有相关关系；
（2）如果体重与身高具有相关关系，求回归直线方程，并预测身高为172cm的女大学生的体重.
见解析
解析:
解：(1)由已知表格中的数据,利用计算器进行计算得：
,
,
,
,
,
,
.
=
≈0.798
由于
,由0.798>0.75知,有很大的把握认为
与
之间具有线性相关关系.
(2) 
与具有线性相关关系,设回归直线方程
,则
关于的回归直线方程为
.
所以对于身高为172cm的女大学生，由回归方程可以预报其体重为：
练习册系列答案
相关题目
从某大学中随机选取8名女大学，其身高与体重的数据如下：
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 身高（cm） | 165 | 165 | 157 | 170 | 175 | 165 | 155 | 170 |
| 体重（kg） | 48 | 57 | 50 | 54 | 64 | 61 | 43 | 59 |
试对其进行残差分析。
从某大学中随机选取8名女大学生，其身高和体重数据如下表所示：
（1）画出散点图，判断x与y是否具有相关关系；
（2）通过计算可知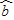
=0.849，
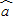=-85.712，请写出y对x的回归直线方程，并计算出编号为2和编号为4的两名学生的体重残差．
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 身高/cm（x） | 165 | 165 | 157 | 170 | 175 | 165 | 155 | 170 |
| 体重/kg（y） | 48 | 57 | 50 | 54 | 64 | 61 | 43 | 59 |
（2）通过计算可知
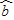=0.849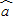，=-85.712，请写出y对x的回归直线方程，并计算出编号为2和编号为4的两名学生的体重残差．