题目内容
已知等差数列{a }中,公差d>0,其前n项和为S
}中,公差d>0,其前n项和为S ,且满足a
,且满足a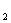 ·a
·a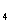 =45,a
=45,a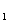 +a
+a =14。
=14。
(Ⅰ)求数列{a }的通项公式及其前n项和S
}的通项公式及其前n项和S ;
;
(Ⅱ)令b =
=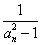 (n∈N*),若数列{c
(n∈N*),若数列{c }满足c
}满足c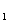 =-
=- ,
,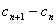 =bn(n∈N*)。求数列{c
=bn(n∈N*)。求数列{c }的通项公式c
}的通项公式c ;
;
(Ⅲ)求f(n)= -
-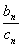 (n∈N*)的最小值。
(n∈N*)的最小值。
(Ⅰ)设数列{a }的公差为d>0,且数列{a
}的公差为d>0,且数列{a }满足a
}满足a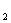 ·a
·a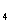 =45,a
=45,a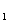 +a
+a =14. 因为数列{a
=14. 因为数列{a }是等差数列,所以a
}是等差数列,所以a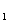 +a
+a = a
= a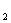 +a
+a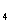 =14.
=14.
因为d>0,所以解方程组 得a
得a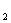 =5,a
=5,a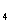 =9. 2分
=9. 2分
所以a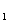 =3,d=2. 所以a
=3,d=2. 所以a =2n+1.
=2n+1.
因为S =na
=na +
+ n(n-1)d,所以S
n(n-1)d,所以S =n2+2n
=n2+2n
数列{a }的通项公式a
}的通项公式a =2n+1,前n项和公式S
=2n+1,前n项和公式S =n2+2n. 5分
=n2+2n. 5分
(Ⅱ)因为b =
=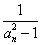 (n∈N*),a
(n∈N*),a =2n+1,所以b
=2n+1,所以b =
= .
.
因为数列{c }满足c
}满足c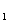 =-
=- ,cn+1-cn=
,cn+1-cn= ,
,
所以cn+1-cn = (
( -
- ). cn- cn+1 =
). cn- cn+1 = (
( -
- )
)
… c2-c1= (1-
(1- )
)
以上各式相加得:cn+1-c1= (1-
(1- )=
)= .
.
因为c1= ,所以
,所以
所以 8分
8分
(Ⅲ)因为f(n)= -
-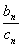 ,b
,b =
= ,c
,c =-
=- ,
,
所以f(n)= +
+ .
.
因为f(n)= +
+ =
= +
+ -
- ,
,
所以 +
+ -
- ≥2
≥2 -
-
f(n)≥ -
- =
= ,当且仅当
,当且仅当 =
= ,即n=2时等号成立.
,即n=2时等号成立.
当n=2时,f(n)最小值为 .
.

练习册系列答案
相关题目
已知x与y 之间的一组数据:则y与x的线性回归方程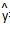 =bx+a必过点 ( )
=bx+a必过点 ( )
A.(1,2) B.(1.5,0) C.(2,2) D.(1.5,4)
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
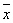 ;
;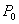 .
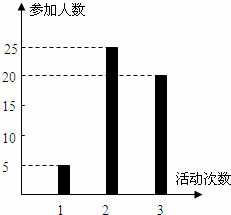
.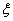 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 .
.
 满足
满足 ,且在
,且在 上的解析式为
上的解析式为 ,则
,则

 B.
B. C.
C.  D.
D. 
 分别是角A,B,C的对边,
分别是角A,B,C的对边, ,且
,且 。
。 的值及△ABC的面积;
的值及△ABC的面积; ,求角C的大小。
,求角C的大小。 在点(1,
在点(1, )处的切线与坐标轴围成的三角面积为 ( )
)处的切线与坐标轴围成的三角面积为 ( )  B.
B. C.
C. D.
D.
 的函数
的函数 对任意的
对任意的 都有
都有 ,且其导函数
,且其导函数 满足:
满足: ,则当
,则当 时,下列成立的是 ( )
时,下列成立的是 ( ) B.
B.
 D.
D.
 的一条渐近线与圆
的一条渐近线与圆
 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( ) C 3 D.4
C 3 D.4