题目内容
按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动(以下简称活动). 该校高2010级一班50名学生在上学期参加活动的次数统计如图所示.
(1)求该班学生参加活动的人均次数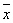 ;
;
(2)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率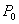 .
.
(3)从该班中任选两名学生,用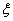 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量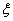 的分布列及数学期望
的分布列及数学期望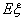 .
.
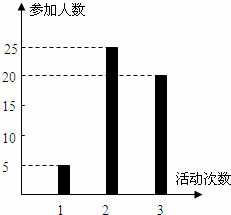
试题解析:由图可知,参加活动1次、2次和3次的学生人数分别为5、25和20.
(I)该班学生参加活动的人均次数为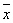 =
= .
.
(II)从该班中任选两名学生,他们参加活动次数恰好相等的概率为
 .
.
(III)从该班中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件 ,“这两人中一人参加2次活动,另一人参加3次活动”为事件
,“这两人中一人参加2次活动,另一人参加3次活动”为事件 ,“这两人中一人参加1次活动,另一人参加3次活动”为事件
,“这两人中一人参加1次活动,另一人参加3次活动”为事件 .易知
.易知
 ;
;
 .
.
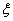 的分布列:
的分布列:
|
| 0 | 1 | 2 |
|
|
|
|
|
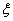 的数学期望:
的数学期望: .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
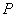



 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列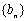 的首项为b,公比为a,其中a,b都是大于1的正整数,且
的首项为b,公比为a,其中a,b都是大于1的正整数,且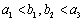 .
. ,总存在
,总存在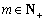 ,使得
,使得 成立,求b的值;
成立,求b的值;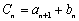 ,问数列
,问数列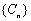 中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
 的图象上所有点向右平移
的图象上所有点向右平移 个单位后得到的图象关于原点对称,则
个单位后得到的图象关于原点对称,则 等于 .
等于 . .那么不等式
.那么不等式 的解集为( ).
的解集为( ). B.
B.
 D.
D.
 的首项
的首项 公差
公差 ,则当n=_________时,前n项和
,则当n=_________时,前n项和 取得最大值.
取得最大值.
 ;
; ,恒有
,恒有 成立,求
成立,求 的取值范围
的取值范围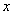 的不等式
的不等式 对
对 恒成立,则
恒成立,则 的取值范围( ).
的取值范围( ). B.
B. C.
C. D.[-12,7]
D.[-12,7]  ,则“
,则“ ”是“
”是“ ”成立的( )
”成立的( ) }中,公差d>0,其前n项和为S
}中,公差d>0,其前n项和为S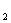 ·a
·a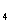 =45,a
=45,a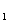 +a
+a =14。
=14。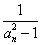 (n∈N*),若数列{c
(n∈N*),若数列{c ,
,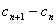 =bn(n∈N*)。求数列{c
=bn(n∈N*)。求数列{c -
-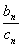 (n∈N*)的最小值。
(n∈N*)的最小值。