题目内容
16.已知数列{an}中,a1=a2=1,且an+2-an=1,则数列{an}的前100项和为2550.分析 an+2-an=1,可得数列{an}的奇数项与偶数项分别成等差数列,公差为1.又a1=a2=1,分组利用等差数列的求和公式即可得出.
解答 解:an+2-an=1,可得数列{an}的奇数项与偶数项分别成等差数列,公差为1.又a1=a2=1,
∴S100=(a1+a3+…+a99)+(a2+a4+…+a100)
=50×1+$\frac{50×49}{2}×1$+50×1+$\frac{50×49}{2}×1$
=2550.
故答案为:2550.
点评 本题考查了等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.在△ABC中,A1,B1分别是边BA,CB的中点,A2,B2分别是线段A1A,B1B的中点,…,An,Bn分别是线段${A_{n-1}}A,{B_{n-1}}B(n∈{N^*},n>1)$的中点,设数列{an},{bn}满足:向量$\overrightarrow{{B_n}{A_n}}={a_n}\overrightarrow{CA}+{b_n}\overrightarrow{CB}(n∈{N^*})$,有下列四个命题,其中假命题是( )
| A. | 数列{an}是单调递增数列,数列{bn}是单调递减数列 | |
| B. | 数列{an+bn}是等比数列 | |
| C. | 数列$\{\frac{a_n}{b_n}\}$有最小值,无最大值 | |
| D. | 若△ABC中,C=90°,CA=CB,则$|\overrightarrow{{B_n}{A_n}}|$最小时,${a_n}+{b_n}=\frac{1}{2}$ |
1.甲、乙、丙、丁、戊5个人排成一排,其中丙必须排在甲、乙之间(不一定相邻),则不同的排法种数为( )
| A. | 80 | B. | 40 | C. | 32 | D. | 16 |
5.当$x∈[-\frac{π}{3},\frac{π}{3}]$时,函数$f(x)=\sqrt{2}sin\frac{x}{4}cos\frac{x}{4}+\sqrt{6}{cos^2}\frac{x}{4}-\frac{{\sqrt{6}}}{2}$的最小值为( )
| A. | $-\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
6.已知R上的奇函数f(x)满足:当x>0时,f(x)=x2+x-1,则f[f(-1)]=( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
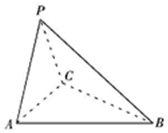 如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.
如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.