题目内容
已知函数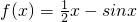 ,其中x∈[0,2π],求函数f(x)的单调区间和最值.
,其中x∈[0,2π],求函数f(x)的单调区间和最值.
解:∵函数y= (x-2sinx),∴y′=
(x-2sinx),∴y′= (1-2cosx).
(1-2cosx).
令y′<0,可得 cosx> .
.
又 x∈[0,2π],故当x∈(0, )或x∈(
)或x∈( ,2π)时,y′<0,函数y单调递减.
,2π)时,y′<0,函数y单调递减.
同理可得,x∈( ,
, ) 时,y′>0,函数y单调递增.
) 时,y′>0,函数y单调递增.
故最小值在x= 或x=2π处取得,
或x=2π处取得,
而当x= 时,函数f(x)的值等于
时,函数f(x)的值等于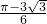 ,当x=2π时,函数f(x)的值等于π,
,当x=2π时,函数f(x)的值等于π,
故当x= 时,函数f(x)有最小值等于
时,函数f(x)有最小值等于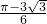 .
.
由题意可得最大值在x=0 或x= 处取得,
处取得,
而当x=0时,函数f(x)的值等于0,当x= 时,函数f(x)的值等于
时,函数f(x)的值等于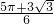 ,
,
故当x= 时,函数f(x)取得最大值等于
时,函数f(x)取得最大值等于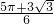 .
.
综上可得,当x= 时,函数f(x)有最小值等于
时,函数f(x)有最小值等于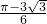 ;
;
当x= 时,函数f(x)取得最大值等于
时,函数f(x)取得最大值等于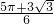 .
.
分析:先求导数,因为是求出单调区间,根据函数的单调区间求出函数的最值.
点评:本题主要考查用导数法求函数的单调区间,尤其要注意三角函数的求导公式以及函数的定义域,根据函数的单调区间求出函数的最值,属于基础题.
 (x-2sinx),∴y′=
(x-2sinx),∴y′= (1-2cosx).
(1-2cosx).令y′<0,可得 cosx>
 .
.又 x∈[0,2π],故当x∈(0,
 )或x∈(
)或x∈( ,2π)时,y′<0,函数y单调递减.
,2π)时,y′<0,函数y单调递减.同理可得,x∈(
 ,
, ) 时,y′>0,函数y单调递增.
) 时,y′>0,函数y单调递增.故最小值在x=
 或x=2π处取得,
或x=2π处取得,而当x=
 时,函数f(x)的值等于
时,函数f(x)的值等于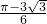 ,当x=2π时,函数f(x)的值等于π,
,当x=2π时,函数f(x)的值等于π,故当x=
 时,函数f(x)有最小值等于
时,函数f(x)有最小值等于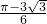 .
.由题意可得最大值在x=0 或x=
 处取得,
处取得,而当x=0时,函数f(x)的值等于0,当x=
 时,函数f(x)的值等于
时,函数f(x)的值等于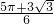 ,
,故当x=
 时,函数f(x)取得最大值等于
时,函数f(x)取得最大值等于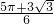 .
.综上可得,当x=
 时,函数f(x)有最小值等于
时,函数f(x)有最小值等于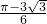 ;
; 当x=
 时,函数f(x)取得最大值等于
时,函数f(x)取得最大值等于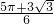 .
.分析:先求导数,因为是求出单调区间,根据函数的单调区间求出函数的最值.
点评:本题主要考查用导数法求函数的单调区间,尤其要注意三角函数的求导公式以及函数的定义域,根据函数的单调区间求出函数的最值,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
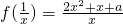 ,其中x∈(0,1]
,其中x∈(0,1] (其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为
,且图象上一个点为 .
. 恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.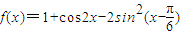 ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移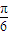 得到函数f(x)的图象
得到函数f(x)的图象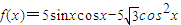 (其中x∈R).
(其中x∈R).