题目内容
(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分7分
已知曲线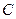 的方程为
的方程为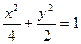 ,
, 、
、 为曲线上的两点,
为曲线上的两点,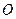 为坐标原点,且有
为坐标原点,且有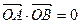 .
.
(1)若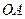 所在直线的方程为
所在直线的方程为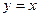 ,求
,求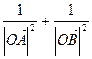 的值;
的值;
(2)若点 为曲线
为曲线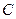 上任意一点,求证:
上任意一点,求证: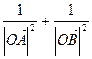 为定值;
为定值;
(3)在(2)的基础上,用类比或推广的方法对新的圆锥曲线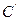 写出一个命题,并对该命题加以证明.
写出一个命题,并对该命题加以证明.
已知曲线
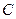 的方程为
的方程为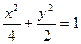 ,
, 、
、 为曲线上的两点,
为曲线上的两点,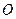 为坐标原点,且有
为坐标原点,且有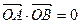 .
.(1)若
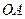 所在直线的方程为
所在直线的方程为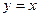 ,求
,求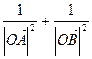 的值;
的值;(2)若点
 为曲线
为曲线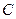 上任意一点,求证:
上任意一点,求证: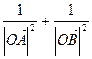 为定值;
为定值;(3)在(2)的基础上,用类比或推广的方法对新的圆锥曲线
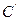 写出一个命题,并对该命题加以证明.
写出一个命题,并对该命题加以证明.解:(1)∵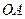 所在直线的方程为
所在直线的方程为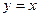
由 可得
可得  ∴
∴ …………2分
…………2分
又 ∵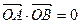 ∴
∴ ∴
∴ 所在直线的方程为
所在直线的方程为 ,
,
同理可得 ……………4分
……………4分
∴ ……………5分
……………5分
(2)当点 在
在 轴上时,点
轴上时,点 在
在 轴上,此时有
轴上,此时有 ,
, ,
,
 ……………6分
……………6分
当点 不在
不在 轴上时,设
轴上时,设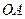 所在直线的方程为
所在直线的方程为 ,则
,则 所在直线的方
所在直线的方 程为
程为 ,
, 、
、 两点的坐标分别为
两点的坐标分别为 、
、
由 可得
可得 , ∴
, ∴  ……………8分
……………8分
同理,由 可得
可得 , ∴
, ∴ ……………9分
……………9分
∴
 为定值………11分
为定值………11分
(3)根据所写新命题的思维层次的不同情况分别进行评分
①已知双曲线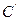 的方程为
的方程为 ,
, 、
、 为曲线上的两点,
为曲线上的两点,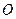 为坐标原点,且有
为坐标原点,且有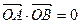 。求证:
。求证: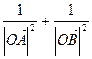 为定值。 ……………13分
为定值。 ……………13分
证明:显然 、
、 两点都不能在
两点都不能在 轴上,
轴上,
设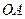 所在直线的方程为
所在直线的方程为 ,则
,则 所在直线的方程为
所在直线的方程为 ,
, 、
、 两点的坐标分别为
两点的坐标分别为 、
、
由
 可得
可得 ,
,  ……………14分
……………14分
同理,由 可得
可得 ,
, 
∴ ………15分
………15分
②已知椭圆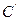 的方程为
的方程为 ,
, 、
、 为曲线上的两点,
为曲线上的两点,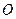 为坐标原
为坐标原 点,且
点,且 有
有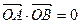 。
。
求证: ……………13分
……………13分
证明:当点 在
在 轴上时,点
轴上时,点 在
在
 轴上,
轴上,
此时有 ,
, ,
,  ……………14分
……………14分
当点 不在
不在 轴上时,设
轴上时,设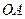 所在直线的方程为
所在直线的方程为 ,
,
则 所在直线的方程为
所在直线的方程为 ,
, 、
、 两点的坐标分别为
两点的坐标分别为 、
、
由 可得
可得 ,
,
 ……………15分
……………15分
同理,由 可得
可得
 , ……………16分
, ……………16分
∴
 …17分
…17分
③已知双曲线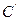 的方程为
的方程为 ,
, 、
、 为曲线上的两点,
为曲线上的两点,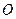 为坐标原点,且有
为坐标原点,且有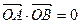 ,
,
则当 时,求证:
时,求证: ……………14分
……………14分
证明:显然 、
、 两点都不能在
两点都不能在 轴上,
轴上,
设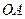 所在直线的方程为
所在直线的方程为 ,则
,则 所
所 在直线的方程为
在直线的方程为 ,
, 、
、 两点的坐标分别为
两点的坐标分别为 、
、
由 可得
可得 ,
,  ……15分
……15分
同理,由 可得
可得
 , ……………17分
, ……………17分
故
 ……………18分
……………18分
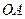 所在直线的方程为
所在直线的方程为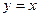
由
 可得
可得  ∴
∴ …………2分
…………2分又 ∵
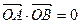 ∴
∴ ∴
∴ 所在直线的方程为
所在直线的方程为 ,
,同理可得
 ……………4分
……………4分∴
 ……………5分
……………5分(2)当点
 在
在 轴上时,点
轴上时,点 在
在 轴上,此时有
轴上,此时有 ,
, ,
, ……………6分
……………6分当点
 不在
不在 轴上时,设
轴上时,设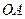 所在直线的方程为
所在直线的方程为 ,则
,则 所在直线的方
所在直线的方 程为
程为 ,
, 、
、 两点的坐标分别为
两点的坐标分别为 、
、
由
 可得
可得 , ∴
, ∴  ……………8分
……………8分同理,由
 可得
可得 , ∴
, ∴ ……………9分
……………9分∴

 为定值………11分
为定值………11分(3)根据所写新命题的思维层次的不同情况分别进行评分
①已知双曲线
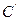 的方程为
的方程为 ,
, 、
、 为曲线上的两点,
为曲线上的两点,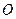 为坐标原点,且有
为坐标原点,且有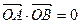 。求证:
。求证: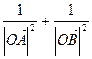 为定值。 ……………13分
为定值。 ……………13分证明:显然
 、
、 两点都不能在
两点都不能在 轴上,
轴上,设
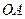 所在直线的方程为
所在直线的方程为 ,则
,则 所在直线的方程为
所在直线的方程为 ,
, 、
、 两点的坐标分别为
两点的坐标分别为 、
、
由

 可得
可得 ,
,  ……………14分
……………14分同理,由
 可得
可得 ,
, 
∴
 ………15分
………15分②已知椭圆
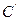 的方程为
的方程为 ,
, 、
、 为曲线上的两点,
为曲线上的两点,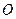 为坐标原
为坐标原 点,且
点,且 有
有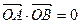 。
。求证:
 ……………13分
……………13分证明:当点
 在
在 轴上时,点
轴上时,点 在
在
 轴上,
轴上,此时有
 ,
, ,
,  ……………14分
……………14分当点
 不在
不在 轴上时,设
轴上时,设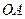 所在直线的方程为
所在直线的方程为 ,
,则
 所在直线的方程为
所在直线的方程为 ,
, 、
、 两点的坐标分别为
两点的坐标分别为 、
、
由
 可得
可得 ,
,  ……………15分
……………15分同理,由
 可得
可得
 , ……………16分
, ……………16分∴

 …17分
…17分③已知双曲线
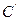 的方程为
的方程为 ,
, 、
、 为曲线上的两点,
为曲线上的两点,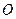 为坐标原点,且有
为坐标原点,且有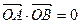 ,
,则当
 时,求证:
时,求证: ……………14分
……………14分证明:显然
 、
、 两点都不能在
两点都不能在 轴上,
轴上,设
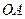 所在直线的方程为
所在直线的方程为 ,则
,则 所
所 在直线的方程为
在直线的方程为 ,
, 、
、 两点的坐标分别为
两点的坐标分别为 、
、
由
 可得
可得 ,
,  ……15分
……15分同理,由
 可得
可得
 , ……………17分
, ……………17分故

 ……………18分
……………18分略

练习册系列答案
相关题目
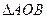 的顶点A在射线
的顶点A在射线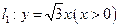 上,
上,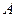 、
、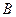 两点关于x轴对称,0为坐标原点,
两点关于x轴对称,0为坐标原点,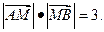 当点A在
当点A在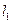 上移动时,记点M的轨迹为W.
上移动时,记点M的轨迹为W.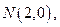 是否存在过
是否存在过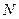 的直线
的直线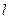 与W相交于P,Q两点,使得
与W相交于P,Q两点,使得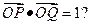 若存在,
若存在,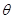 是三角形的一个内角,且
是三角形的一个内角,且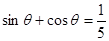 ,则方程
,则方程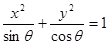 所表示的曲线为( ).
所表示的曲线为( ).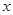 轴上的椭圆
轴上的椭圆 轴上的椭圆
轴上的椭圆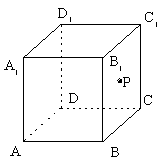
 ,点
,点 的坐标为(1,1),点
的坐标为(1,1),点 在抛物线
在抛物线 上运动,点
上运动,点 满足
满足 ,经过
,经过
 轴垂直的直线交抛物线于点
轴垂直的直线交抛物线于点 满足
满足 ,求点
,求点
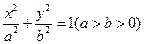 的焦点分别为
的焦点分别为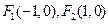 ,
,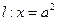 交
交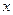 轴于于点A,且
轴于于点A,且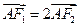 。
。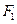 、
、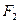 分别作互相垂直的两直线与椭圆分别
分别作互相垂直的两直线与椭圆分别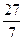 ,求DE的直线方程。
,求DE的直线方程。 ,则双曲线方程为___________。
,则双曲线方程为___________。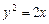 与过焦点的直线交于A、
与过焦点的直线交于A、 B
B 两点,则
两点,则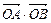 =" " .
=" " .