题目内容
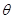 是三角形的一个内角,且
是三角形的一个内角,且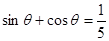 ,则方程
,则方程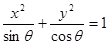 所表示的曲线为( ).
所表示的曲线为( ).A.焦点在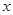 轴上的椭圆 轴上的椭圆 | B.焦点在 轴上的椭圆 轴上的椭圆 |
C.焦点在 轴上的双曲线 轴上的双曲线 | D.焦点在 轴上的的双曲线 轴上的的双曲线 |
C
分析:把 sinθ+cosθ=
 两边平方可得,sinθ?cosθ="-"
两边平方可得,sinθ?cosθ="-"  <0,可判断θ为钝角,cosθ<0,从而判断方程所表示的曲线.
<0,可判断θ为钝角,cosθ<0,从而判断方程所表示的曲线.解:因为θ∈(0,π),且sinθ+cosθ=
 ,所以,θ∈(
,所以,θ∈(  ,π),
,π),且|sinθ|>|cosθ|,所以θ∈(
 ,
, ),从而cosθ<0,
),从而cosθ<0,从而
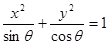 表示焦点在x轴上的椭圆.
表示焦点在x轴上的椭圆.故选C.

练习册系列答案
相关题目
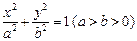 的左、右焦点,点P(-1,
的左、右焦点,点P(-1,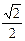 )在椭圆上,线段PF2与
)在椭圆上,线段PF2与 轴的交点
轴的交点 满足
满足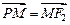 .(1)求椭圆的标准方程;
.(1)求椭圆的标准方程; 轴重合的直线
轴重合的直线 ,
,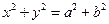 相交于A、B.并与椭圆相交于C、D.当
相交于A、B.并与椭圆相交于C、D.当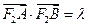 ,且
,且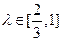 时,求△F2CD的面积S的取值范围.
时,求△F2CD的面积S的取值范围. 的方程为
的方程为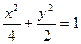 ,
, 、
、 为曲线上的两点,
为曲线上的两点,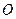 为坐标原点,且有
为坐标原点,且有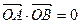 .
. 所在直线的方程为
所在直线的方程为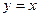 ,求
,求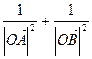 的值;
的值; 写出一个命题,并对该命题加以证明.
写出一个命题,并对该命题加以证明. 为双曲线
为双曲线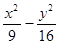 =1的右支上一点,
=1的右支上一点,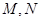 分别是圆
分别是圆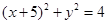 和
和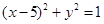 上的点,则
上的点,则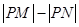 的最大值为
的最大值为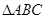 的顶点
的顶点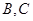 为
为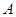 的双曲线,若
的双曲线,若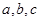 ,且
,且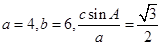 ,
,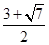
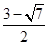
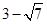
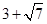
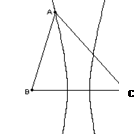
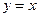 与抛物线C相交
与抛物线C相交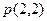 是AB的中点,则抛物线C的方程为_______________.
是AB的中点,则抛物线C的方程为_______________.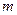 为常数,若点
为常数,若点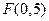 是双曲线
是双曲线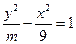 的一个焦点,则
的一个焦点,则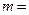 。
。 中,
中, 且
且 ,设
,设 ,以
,以 、
、 为焦点且过点
为焦点且过点 的双曲线的离心率为
的双曲线的离心率为 ,以
,以 、
、 ,则
,则 =__________
=__________
 y中,点A(
y中,点A( 4,0)、B(1,0),动点P满足
4,0)、B(1,0),动点P满足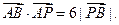
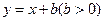 与轨迹C相交于M、N两点,直线
与轨迹C相交于M、N两点,直线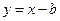 与轨迹C相交于P、Q
与轨迹C相交于P、Q 次连接M,N,P,Q得到的四边形MNPQ是棱形,求b。
次连接M,N,P,Q得到的四边形MNPQ是棱形,求b。