题目内容
若 是
是 >0)图象的一条对称轴,当ω取最小值时
>0)图象的一条对称轴,当ω取最小值时
- A.f(x) 在
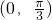 上单调递增
上单调递增 - B.f(x) 在
 上单调递减
上单调递减 - C.f(x) 在
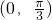 上单调递减
上单调递减 - D.f(x) 在
 上单调递增
上单调递增
D
分析:由于f(x)=2sin(ωx+ ),利用
),利用 ω+
ω+ =kπ+
=kπ+ (k∈Z)可求得ω的最小值,从而可得答案.
(k∈Z)可求得ω的最小值,从而可得答案.
解答:∵f(x)= sinωx+cosωx=2sin(ωx+
sinωx+cosωx=2sin(ωx+ ),
),
∵x= 是f(x)的图象的一条对称轴,
是f(x)的图象的一条对称轴,
∴ ω+
ω+ =kπ+
=kπ+ (k∈Z),
(k∈Z),
∴ω=6k+2,又ω>0,
∴ωmin=2.
∴f(x)=2sin(2x+ ),
),
∴当2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,即kπ-
,即kπ- ≤x≤2kπ+
≤x≤2kπ+ (k∈Z)时单调递增,
(k∈Z)时单调递增,
当2kπ+ ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ 即kπ+
即kπ+ ≤x≤kπ+
≤x≤kπ+ (k∈Z)时单调递减,
(k∈Z)时单调递减,
显然,当k=0时,f(x)在[- ,
, ]上单调递增,在[
]上单调递增,在[ ,
, ]上单调递减,故D正确,A,B,C均错误.
]上单调递减,故D正确,A,B,C均错误.
故选D.
点评:本题考查两角和与差的三角函数的性质,考查正弦函数的性质,求得ω的最小值是关键,也是难点,属于中档题.
分析:由于f(x)=2sin(ωx+
 ),利用
),利用 ω+
ω+ =kπ+
=kπ+ (k∈Z)可求得ω的最小值,从而可得答案.
(k∈Z)可求得ω的最小值,从而可得答案.解答:∵f(x)=
 sinωx+cosωx=2sin(ωx+
sinωx+cosωx=2sin(ωx+ ),
),∵x=
 是f(x)的图象的一条对称轴,
是f(x)的图象的一条对称轴,∴
 ω+
ω+ =kπ+
=kπ+ (k∈Z),
(k∈Z),∴ω=6k+2,又ω>0,
∴ωmin=2.
∴f(x)=2sin(2x+
 ),
),∴当2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,即kπ-
,即kπ- ≤x≤2kπ+
≤x≤2kπ+ (k∈Z)时单调递增,
(k∈Z)时单调递增,当2kπ+
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ 即kπ+
即kπ+ ≤x≤kπ+
≤x≤kπ+ (k∈Z)时单调递减,
(k∈Z)时单调递减,显然,当k=0时,f(x)在[-
 ,
, ]上单调递增,在[
]上单调递增,在[ ,
, ]上单调递减,故D正确,A,B,C均错误.
]上单调递减,故D正确,A,B,C均错误.故选D.
点评:本题考查两角和与差的三角函数的性质,考查正弦函数的性质,求得ω的最小值是关键,也是难点,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 抛物线有光学性质:由其焦点射出的光线经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然.如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴.开口向右.一光源在点M处,由其发出一条平行于x轴的光线射向抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M.
抛物线有光学性质:由其焦点射出的光线经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然.如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴.开口向右.一光源在点M处,由其发出一条平行于x轴的光线射向抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M.