题目内容
(本题满分13分)如图,菱形ABCD中,∠ABC=60o, AE⊥平面ABCD,CF⊥平面ABCD,AB= AE=2,CF=3.
(Ⅰ)求证EF⊥平面BDE;
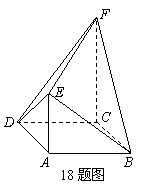 (Ⅱ)求锐二面角E—BD—F的大小.
(Ⅱ)求锐二面角E—BD—F的大小.
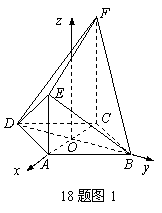
(Ⅰ)证法一:连接AC、BD,设AC∩BD=O,
∵ABCD为菱形,∴AC⊥BD,以O为原点,OA,OB为x、y轴正向,z轴过O且平行于CF,建立空间直角坐标系(图1),……2分
则![]() ,
,
![]() ,
,![]() ,…………4分
,…………4分
∴ ![]() ,
,![]() ,
,
∴EF⊥DE,EF⊥BE,又DE∩BE=E,∴EF⊥平面BDE.………6分
(Ⅱ)解法一:由知(Ⅰ)![]() 是平面BDE的一个法向量,
是平面BDE的一个法向量,
设![]() 是平面BDF的一个法向量,
是平面BDF的一个法向量,
![]() ,由
,由![]()
得: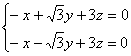 ,取x=3,得z=1,y=0,
,取x=3,得z=1,y=0,
于是![]() ,……………………………………………………………………………10分
,……………………………………………………………………………10分
![]() ,…………………………………………12分
,…………………………………………12分
但二面角E—BD—F为锐二面角,故其大小为45o. ………………………………………13分
(Ⅰ)证法二:连接AC、BD,设AC∩BD=O, (图2)
∵ABCD为菱形, ∴AC⊥BD,
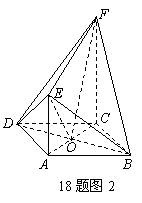 ∵CF⊥平面ABCD,∴CF⊥BD,AC∩CF=C,
∵CF⊥平面ABCD,∴CF⊥BD,AC∩CF=C,
∴BD⊥平面ACF,EFÌ平面ACF,∴BD⊥EF,……2分
![]() ,
,![]() ,
,
![]() ,∴
,∴![]() ,
,
∴ ![]() , ……………………………………………4分
, ……………………………………………4分
又BD∩OE=O,∴EF⊥平面BDE.…………………………6分
(Ⅱ)解法二:由(Ⅰ)BD⊥平面ACF,OEÌ平面ACF,OFÌ平面ACF,
∴OE⊥BD,OF⊥BD,∴∠EOF是二面角E—BD—F的一个平面角, ………………10分
又![]() ,
,![]() ,∴∠EOF=45o,即二面角E—BD—F的大小为45o.…13分
,∴∠EOF=45o,即二面角E—BD—F的大小为45o.…13分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在城
在城 的南偏西
的南偏西 的方向上,由
的方向上,由 ,在
,在 处,有一人正沿公路向
处,有一人正沿公路向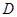 处,此时
处,此时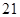 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达
 中,
中,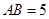 ,
, ,
, ,
, ,
, ,
, 是
是 的中点,设
的中点,设 ,
, ,
, .
.
 表示
表示 ;
; 的长.
的长.
 ,
, ,底面
,底面 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD,  ,O为AD中点.
,O为AD中点.
 与平面
与平面 所成角的余弦值;
所成角的余弦值; 点到平面
点到平面 的距离
的距离 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 中,已知
中,已知
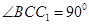 ,
,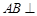 侧面
侧面

 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).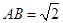 ,求二面角
,求二面角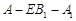 的大小.
的大小.