题目内容
设a>0,b>0,a+b=1.求证:(1)![]() ≥8;
≥8;
(2)(a+![]() )2+(b+
)2+(b+![]() )2≥
)2≥![]() .
.
思路分析:要证的不等式是在已知条件下成立的,从不等式的结构及与已知的关系考虑,可用综合法证之.
证明:(1)∵a>0,b>0,a+b=1,∴![]() ≥4.
≥4.
∴![]() +
+![]() +
+![]() =(a+b)(
=(a+b)(![]() +
+![]() )+
)+![]() ≥
≥![]() ·2
·2![]() +4=8.
+4=8.
∴![]() +
+![]() +
+![]() ≥8.
≥8.
(2)∵![]() ≤
≤![]() ,则
,则![]() .
.
∴(a+![]() )2+(b+
)2+(b+![]() )2≥2(
)2≥2(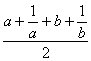 )2=
)2=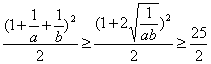 .
.
∴(a+![]() )2+(b+
)2+(b+![]() )2≥
)2≥![]()
深化升华 利用综合法证明不等式可利用已经证过的不等式作为基础,再运用不等式的性质推导出所要证的不等式.但要注意防止在推证中盲目套用公式和错用性质,要把握住不等号方向始终如一的正确性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目