题目内容
过椭圆
内一点M（2，1）引一条弦，使弦被M点平分，求这条弦所在直线的方程．
【答案】分析：设出直线与椭圆的交点坐标，代入椭圆方程，利用点差法，结合M（2，1）为AB的中点吗，求出直线的斜率，即可得到直线的方程．
解答：解：设直线与椭圆的交点为A（x1，y1）、B（x2，y2）
∵M（2，1）为AB的中点
∴x1+x2=4，y1+y2=2
∵又A、B两点在椭圆上，则
，
两式相减得
于是（x1+x2）（x1-x2）+4（y1+y2）（y1-y2）=0
∴
，即
，
故所求直线的方程为
，即x+2y-4=0．
点评：本题考查直线与椭圆的位置关系，考查点差法的运用，考查学生的计算能力，属于中档题．
解答：解：设直线与椭圆的交点为A（x1，y1）、B（x2，y2）
∵M（2，1）为AB的中点
∴x1+x2=4，y1+y2=2
∵又A、B两点在椭圆上，则
，两式相减得
于是（x1+x2）（x1-x2）+4（y1+y2）（y1-y2）=0
∴
，即，故所求直线的方程为
，即x+2y-4=0．点评：本题考查直线与椭圆的位置关系，考查点差法的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
内一点M（2，1）引一条弦，使弦被M点平分，求这条弦所在直线的方程．
内一点M（2，1）引一条弦，使该弦被点M平分，求这条弦所在直线l的方程。 
内一点M（2，1）引一条弦，使得弦被M点平分，求此弦所在的直线方程．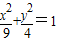
内一点M（2，0）引椭圆的动弦AB，则弦AB的中点N的轨迹方程是 ．