题目内容
过椭圆
内一点M（2，1）引一条弦，使该弦被点M平分，求这条弦所在直线l的方程。
内一点M（2，1）引一条弦，使该弦被点M平分，求这条弦所在直线l的方程。 解：设直线l与椭圆的交点为A（x1，y1），B（x2，y2），因为M为AB的中点，
所以x1+x2=4，y1+y2=2，
又A，B两点在椭圆上，则有
，
两式相减，得
所以
，即
，
此时直线l的方程为x+2y-4=0，代入椭圆的方程，△>0，
故所求直线l的方程为x+2y-4=0。
所以x1+x2=4，y1+y2=2，
又A，B两点在椭圆上，则有
，两式相减，得
所以
，即，此时直线l的方程为x+2y-4=0，代入椭圆的方程，△>0，
故所求直线l的方程为x+2y-4=0。
练习册系列答案
相关题目
内一点M（2，1）引一条弦，使弦被M点平分，求这条弦所在直线的方程．
内一点M（2，1）引一条弦，使弦被M点平分，求这条弦所在直线的方程．
内一点M（2，1）引一条弦，使得弦被M点平分，求此弦所在的直线方程．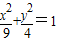
内一点M（2，0）引椭圆的动弦AB，则弦AB的中点N的轨迹方程是 ．