题目内容
（2009•武汉模拟）在△ABC中，|AB|=3，|AC|=4，|BC|=5，O为△ABC的内心，且
=λ
+μ
，则λ+μ=
．
| AO |
| AB |
| BC |
| 5 |
| 6 |
| 5 |
| 6 |
分析：根据三角形是直角三角形，得到它的内心的位置，从而表示出向量
，根据向量之间的加减关系，写出向量与要求两个向量之间的关系，得到两个系数的值，求和得到结果．
| AO |
解答：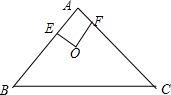
解：设内切圆半径为r．
由题意得：r=OE=OF=AE=AF=
=
=1．
所以：
=
+
=
+
=
+
(
+
)
=
+
．
∴λ=
，μ=
．
∴λ+μ=
+
=
．
故答案为：
．
解：设内切圆半径为r．由题意得：r=OE=OF=AE=AF=
| a+b-c |
| 2 |
| 3+4-5 |
| 2 |
所以：
| AO |
| AE |
| AF |
=
| 1 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
=
| 1 |
| 3 |
| AB |
| 1 |
| 4 |
| AB |
| BC |
=
| 7 |
| 12 |
| AB |
| 1 |
| 4 |
| BC |
∴λ=
| 7 |
| 12 |
| 1 |
| 4 |
∴λ+μ=
| 7 |
| 12 |
| 1 |
| 4 |
| 5 |
| 6 |
故答案为：
| 5 |
| 6 |
点评：用一组向量来表示一个向量，是以后解题过程中常见到的，向量的加减运算是用向量解决问题的基础，要学好运算，才能用向量解决立体几何问题，三角函数问题，好多问题都是以向量为载体的．
练习册系列答案
习题精选系列答案
相关题目
（2009•武汉模拟）（文科做） 如图，在边长为a的正方体ABCD-A1B1C1D1中M、N、P、Q分别为AD，CD，BB1，C1D1的中点