题目内容
甲、乙等![]() 名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为
名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为![]() ).
).
(Ⅰ)求甲、乙两考生的面试序号至少有一个为奇数的概率;
(Ⅱ)记在甲、乙两考生之间参加面试的考生人数为![]() ,求随机变量
,求随机变量![]() 的分布列与期望.
的分布列与期望.
【命题意图】本题考查概率知识,分布列和期望的求法,考查学生应用知识解决问题的能力,中等题.
【答案】(Ⅰ)只考虑甲、乙两考生的相对位置,用组合计算基本事件数;
设A表示“甲、乙的面试序号至少有一个为奇数”,则![]() 表示“甲、乙的序号均为偶数”,
表示“甲、乙的序号均为偶数”,
由等可能性事件的概率计算公式得: ![]()
甲、乙两考生的面试序号至少有一个为奇数的概率是![]() . ………………6分
. ………………6分
(另解![]() )
)
(Ⅱ)随机变量![]() 的所有可能取值是0,1,2,3,4,
的所有可能取值是0,1,2,3,4,
且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
[另解:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ]………………………………………………10分
]………………………………………………10分
所以随机变量![]() 的分布列是:
的分布列是:
|
| 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
所以![]()
即甲、乙两考生之间的面试考生个数![]() 的期望值是
的期望值是![]() . ………………12分
. ………………12分

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
某学校高一(1)班甲、乙两名同学参加最近5次数学考试的成绩(单位:分)统计如下:
|
甲: |
65 |
94 |
95 |
98 |
98 |
|
乙: |
62 |
71 |
98 |
99 |
100 |
(1)分别写出甲、乙成绩的平均分和中位数.
(2)分别用平均分和中位数解释甲、乙两位同学哪位同学的成绩较好.
(3)又知同班同学丙的最近5次数学测试成绩(单位:分)如下:
|
丙: |
80 |
86 |
90 |
95 |
99 |
分别用平均分、中位数和成绩波动大小等知识解释甲与丙的成绩谁的好.说明理由.
某学校高一
(1)班甲、乙两名同学参加最近5次数学考试的成绩(单位:分)统计如下:|
甲: |
65 |
94 |
95 |
98 |
98 |
|
乙: |
62 |
71 |
98 |
99 |
100 |
(1)
分别写出甲、乙成绩的平均分和中位数.(2)
分别用平均分和中位数解释甲、乙两位同学哪位同学的成绩较好.(3)
又知同班同学丙的最近5次数学测试成绩(单位:分)如下:|
丙: |
80 |
86 |
90 |
95 |
99 |
分别用平均分、中位数和成绩波动大小等知识解释甲与丙的成绩谁的好.说明理由.
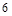 名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为
名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为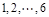 ).
).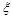 ,求随机变量
,求随机变量