题目内容
已知数列 ,则a1+a100=________,a1+a2+a3+a4+…+a99+a100=________.
,则a1+a100=________,a1+a2+a3+a4+…+a99+a100=________.
100 5000
分析:由数列的通项公式可得数列的前100项中奇数项分别为:0,2,4,…98;偶数项分别为:2,4,6,…100
从而可求a1+a100;而a1+a2+a3+a4+…+a99+a100=(a1+a3+…a99)+(a2+a4+…+a100),利用等差数列的求和公式可求
解答:由数列的通项公式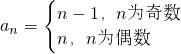
可得数列的前100项中奇数项分别为:0,2,4,…98;偶数项分别为:2,4,6,…100
∴a1+a100=0+100=100
∵a1+a2+a3+a4+…+a99+a100=(a1+a3+…a99)+(a2+a4+…+a100)
=(0+2+4+…+98)+(2+4+…+100)
=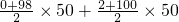 =5000
=5000
故答案为:100,5000
点评:本题主要考查了由数列的通项公式求解数列的和,解题的关键是由通项公式发现数列的奇数项和偶数项分别组成等差数列,结合等差数列的求和公式可进行求解
分析:由数列的通项公式可得数列的前100项中奇数项分别为:0,2,4,…98;偶数项分别为:2,4,6,…100
从而可求a1+a100;而a1+a2+a3+a4+…+a99+a100=(a1+a3+…a99)+(a2+a4+…+a100),利用等差数列的求和公式可求
解答:由数列的通项公式
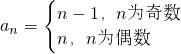
可得数列的前100项中奇数项分别为:0,2,4,…98;偶数项分别为:2,4,6,…100
∴a1+a100=0+100=100
∵a1+a2+a3+a4+…+a99+a100=(a1+a3+…a99)+(a2+a4+…+a100)
=(0+2+4+…+98)+(2+4+…+100)
=
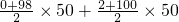 =5000
=5000故答案为:100,5000
点评:本题主要考查了由数列的通项公式求解数列的和,解题的关键是由通项公式发现数列的奇数项和偶数项分别组成等差数列,结合等差数列的求和公式可进行求解

练习册系列答案
相关题目
已知数列1,a1,a2,9是等差数列,数列1,b1,b2,b3,9是等比数列,则b2?(a1+a2)=( )
| A、20 | B、30 | C、35 | D、40 |
 的值是( )
的值是( )

 或-
或-
