题目内容
在数列{an}中,a1=2,an+1=an+2n+1(n∈N*)
(1)求证:数列{an-2n}为等差数列;
(2)设数列{bn}满足bn=log2(an+1-n),若 …
… 对一切n∈N*且n≥2恒成立,求实数k的取值范围.
对一切n∈N*且n≥2恒成立,求实数k的取值范围.
解:(1)(an+1-2n+1)-(an-2n)=an+1-an-2n=1
故数列{an-2n}为等差数列,且公差d=1.
an-2n=(a1-2)+(n-1)d=n-1,an=2n+n-1;
(2)由(1)可知an=2n+n-1,∴bn=log2(an+1-n)=n
设f(n)= …(1+
…(1+ )×
)×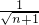 ,(n≥2)
,(n≥2)
则f(n+1)= …(1+
…(1+ )×(1+
)×(1+ )×
)× ,
,
两式相除可得 =(1+
=(1+ )×
)× =
= >1,
>1,
则有f(n)>f(n-1)>f(n-2)>…>f(2)= ,
,
要使 …
… 对一切n∈N*且n≥2恒成立,
对一切n∈N*且n≥2恒成立,
必有k< ;
;
故k的取值范围是k< .
.
分析:(1)先对关系式an+1=an+2n+1整理可得到)(an+1-2n+1)-(an-2n)=an+1-an-2n=1,即数列{an-2n}为等差数列,
(2)根据(1)可求出数列{an-2n}的通项公式,即可得到数列{an}的通项公式,根据bn=log2(an+1-n),可得到bn的表达式,设f(n)= …(1+
…(1+ )×
)×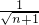 ,分析可得f(n)的最小值,结合题意即可得答案.
,分析可得f(n)的最小值,结合题意即可得答案.
点评:本小题主要考查数列、数学归纳法和不等式的有关知识,考查推理论证、抽象概括、运算求解和探究能力,考查学生是否具有审慎思维的习惯和一定的数学视野.
故数列{an-2n}为等差数列,且公差d=1.
an-2n=(a1-2)+(n-1)d=n-1,an=2n+n-1;
(2)由(1)可知an=2n+n-1,∴bn=log2(an+1-n)=n
设f(n)=
 …(1+
…(1+ )×
)×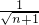 ,(n≥2)
,(n≥2)则f(n+1)=
 …(1+
…(1+ )×(1+
)×(1+ )×
)× ,
,两式相除可得
 =(1+
=(1+ )×
)× =
= >1,
>1,则有f(n)>f(n-1)>f(n-2)>…>f(2)=
 ,
,要使
 …
… 对一切n∈N*且n≥2恒成立,
对一切n∈N*且n≥2恒成立,必有k<
 ;
;故k的取值范围是k<
 .
.分析:(1)先对关系式an+1=an+2n+1整理可得到)(an+1-2n+1)-(an-2n)=an+1-an-2n=1,即数列{an-2n}为等差数列,
(2)根据(1)可求出数列{an-2n}的通项公式,即可得到数列{an}的通项公式,根据bn=log2(an+1-n),可得到bn的表达式,设f(n)=
 …(1+
…(1+ )×
)×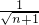 ,分析可得f(n)的最小值,结合题意即可得答案.
,分析可得f(n)的最小值,结合题意即可得答案.点评:本小题主要考查数列、数学归纳法和不等式的有关知识,考查推理论证、抽象概括、运算求解和探究能力,考查学生是否具有审慎思维的习惯和一定的数学视野.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.