题目内容
设△ABC的内角A,B,C的对边为a,b,c ,且满足:b2+c2=a2+bc。
(1)若acosB+bcosA=2csinC,求角C的大小;
(2)若△ABC的面积为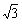 ,其外接圆的半径为
,其外接圆的半径为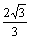 ,求△ABC的周长。
,求△ABC的周长。
(1)若acosB+bcosA=2csinC,求角C的大小;
(2)若△ABC的面积为
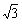 ,其外接圆的半径为
,其外接圆的半径为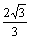 ,求△ABC的周长。
,求△ABC的周长。 解:(1)∵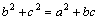 ,
,
∴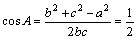 ,
,
又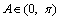 ,
,
∴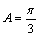 ,
,
又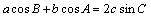 ,
,
由正弦定理,得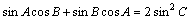 ,
,
∴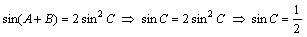 ,
,
故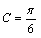 。
。
(2)由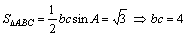 ,
,
由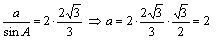 ,
,
∴ ,故
,故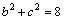 ,
,
∴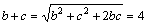 ,
,
∴△ABC的周长为:a+b+c=6。
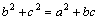 ,
,∴
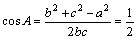 ,
,又
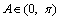 ,
,∴
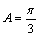 ,
,又
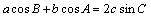 ,
,由正弦定理,得
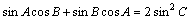 ,
,∴
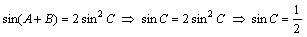 ,
,故
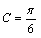 。
。(2)由
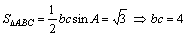 ,
,由
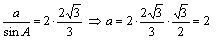 ,
,∴
 ,故
,故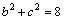 ,
,∴
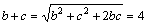 ,
,∴△ABC的周长为:a+b+c=6。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目