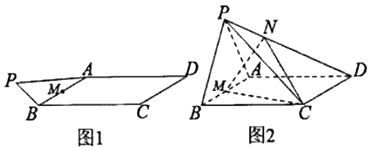
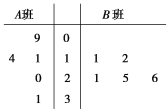
题目内容
【题目】为鼓励居民节约用水,某市自来水公司对全市用户采用分段计费的方式计算水费,收费标准如下:不超过![]() 的部分为2.20元/
的部分为2.20元/![]() ;超过
;超过![]() 不超过
不超过![]() 的部分为2.80元/
的部分为2.80元/![]() ;超过
;超过![]() 部分为3.20元/
部分为3.20元/![]() .
.
(1)试求居民月水费y(元)关于用水量![]() 的函数关系式;
的函数关系式;
(2)某户居民4月份用水![]() ,应交水费多少元?
,应交水费多少元?
(3)若有一户居民5月份水费为57.20元,请问该户居民5月份用水多少?
(4)若某户居民6月份、7月份共用水![]() ,且6月份水费比7月份水费少12元,则该户居民6、7月份各用水多少?
,且6月份水费比7月份水费少12元,则该户居民6、7月份各用水多少?
【答案】(1)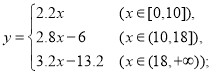 (2)38.8元;(3)22吨;(4)6月16吨,7月20吨
(2)38.8元;(3)22吨;(4)6月16吨,7月20吨
【解析】
(1)根据![]() 的不同取值范围列出不同的表达式,得水费函数
的不同取值范围列出不同的表达式,得水费函数![]() ;
;
(2)![]() 代入解析式可得;
代入解析式可得;
(3)可求出![]() 在
在![]() 的不同范围内的取值范围,然后列式
的不同范围内的取值范围,然后列式![]() 计算;
计算;
(4)两个月共用水36吨,说明一个月比18吨多,一个月比16吨少,但都不会少于10吨,又6月份水费少,因此6月份少于18吨,7月份多于18吨,由此列方程可得.
(1)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
综上, .
.
(2)![]() 时,
时,![]() (元);
(元);
(3)由(1)![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() (吨);
(吨);
(4)两个月共用水36吨,说明一个月比18吨多,一个月比18吨少,
设6月份用水![]() 吨,因为6月份水费少,则
吨,因为6月份水费少,则![]() ,又因为
,又因为![]() ,显然
,显然![]() ,
,
所以![]() ,解得
,解得![]() .
.
所以6月份用水16吨.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某商店为了解气温对某产品销售量的影响,随机记录了该商店![]() 月份中
月份中![]() 天的日销售量
天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:℃)的数据,如表所示:
(单位:℃)的数据,如表所示:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 与
与![]() 的回归方程
的回归方程![]() :
:
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月份某天的最低气温为
月份某天的最低气温为![]() ,请用(1)中的回归方程预测该商店当日的销售量.
,请用(1)中的回归方程预测该商店当日的销售量.
参考公式: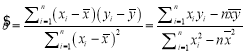 ,
,![]() .
.