题目内容
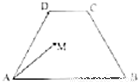
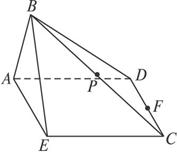
如图(1),等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图(2),将△ABE沿AE折起,使二面角B-AE-C成直二面角,连结BC,BD,F是CD的中点,P是棱BC的中点.
(1) (2)
(1)求证:AE⊥BD;
(2)求证:平面PEF⊥平面AECD;
(3)判断DE能否垂直于平面ABC?并说明理由.
解:(1)证明:连结BD,取AE中点M,连结BM,DM.
∵在等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点,
∴△ABE与△ADE都是等边三角形.∴BM⊥AE,DM⊥AE.
∵BM∩DM=M,BM,DM![]() 平面BDM,∴AE⊥平面BDM.
平面BDM,∴AE⊥平面BDM.
∵BD![]() 平面BDM,∴AE⊥BD.
平面BDM,∴AE⊥BD.
(2)证明:连结CM交EF于点N,连结PN.
∵ME∥FC,且ME=FC,∴四边形MECF是平行四边形.
∴N是线段CM的中点.∵P是线段BC的中点,∴PN∥BM.
∵BM⊥平面AECD,∴PN⊥平面AECD.
又∵PN![]() 平面PEF,∴平面PEF⊥平面AECD.
平面PEF,∴平面PEF⊥平面AECD.
(3)DE与平面ABC不垂直.
证明:假设DE⊥平面ABC,则DE⊥AB.
∴BM⊥平面AECD.∴BM⊥DE.
∵AB∩BM=B,AB,BM![]() 平面ABE,∴DE⊥平面ABE.
平面ABE,∴DE⊥平面ABE.
∴DE⊥AE,这与∠AED=60°矛盾.∴DE与平面ABC不垂直.

练习册系列答案
相关题目
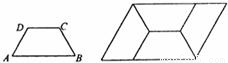
 如图,四边形ABCD是等腰梯形,AB∥CD,且AD=CD=1.由4个这样的等腰梯形可以拼出图乙所示的平行四边形,则该平行四边形的面积为
如图,四边形ABCD是等腰梯形,AB∥CD,且AD=CD=1.由4个这样的等腰梯形可以拼出图乙所示的平行四边形,则该平行四边形的面积为 如图所示,在等腰梯形ABCD中,AB∥DC,AB=3,DC=1,tanB=2,点M是梯形ABCD内(含边界)的一个动点,则
如图所示,在等腰梯形ABCD中,AB∥DC,AB=3,DC=1,tanB=2,点M是梯形ABCD内(含边界)的一个动点,则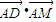 的最大值是 .
的最大值是 .