题目内容
如图所示,在等腰梯形ABCD中,AB∥DC,AB=3,DC=1,tanB=2,点M是梯形ABCD内(含边界)的一个动点,则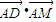 的最大值是 .
的最大值是 .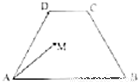
【答案】分析:以A点为坐标原点,AB所在直线为x轴,建立坐标系,然后表示出 ,求出最值即可.
,求出最值即可.
解答:解:以A点为坐标原点,AB所在直线为x轴,建立如图坐标系,可得
A(0,0),B(3,0),C(2,2),D(1,2),
则直线BC方程为y=-2x+6
设M(λ,-2λ+6),(2≤λ≤3)
可得则 =(λ,-2λ+6),
=(λ,-2λ+6), =(1,2),
=(1,2),
∴ =λ+2(-2λ+6)=12-3λ
=λ+2(-2λ+6)=12-3λ
∵2≤λ≤3,
∴当λ=2时, =6取得最大值.
=6取得最大值.
故答案为:6
点评:本题主要考查了平面向量数量积的含义与物理意义,以及利用解析法求解向量问题,同时考查了计算能力和分析问题的能力,属于基础题.
 ,求出最值即可.
,求出最值即可.解答:解:以A点为坐标原点,AB所在直线为x轴,建立如图坐标系,可得

A(0,0),B(3,0),C(2,2),D(1,2),
则直线BC方程为y=-2x+6
设M(λ,-2λ+6),(2≤λ≤3)
可得则
 =(λ,-2λ+6),
=(λ,-2λ+6), =(1,2),
=(1,2),∴
 =λ+2(-2λ+6)=12-3λ
=λ+2(-2λ+6)=12-3λ∵2≤λ≤3,
∴当λ=2时,
 =6取得最大值.
=6取得最大值.故答案为:6
点评:本题主要考查了平面向量数量积的含义与物理意义,以及利用解析法求解向量问题,同时考查了计算能力和分析问题的能力,属于基础题.

练习册系列答案
相关题目
 如图所示,在等腰梯形ABCD中,AB∥DC,AB=3,DC=1,tanB=2,点M是梯形ABCD内(含边界)的一个动点,则
如图所示,在等腰梯形ABCD中,AB∥DC,AB=3,DC=1,tanB=2,点M是梯形ABCD内(含边界)的一个动点,则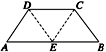
 中,
中, ,
, ,
, 为
为 中点.将
中点.将 沿
沿 折起至
折起至 ,使得平面
,使得平面 平面
平面 ,
, 分别为
分别为 的中点.
的中点. 面
面 ;
; 的余弦值.
的余弦值.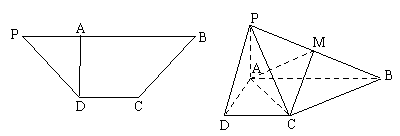 (2)若
(2)若