题目内容
如图，四边形ABCD是等腰梯形，AB∥CD，且AD=CD=1．由4个这样的等腰梯形可以拼出图乙所示的平行四边形，则该平行四边形的面积为 ．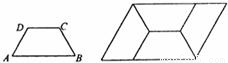
【答案】分析：由于上底和两腰长已知，故要求梯形面积，关键是要找出底边上和高，由于图形中无法再分析出边与边的关系，所以我们可以从角的方向入手，求梯形的内角，进一步求出梯形的其它未知边长，进而求解平行四边形的面积．
解答：解：设等腰梯形的底角为θ，
则由图可知，θ+θ+θ=180°，即θ=60°．
由AD=CD=1知，
AB=CD+2AD•cos60°=2，
故梯形的面积为
=
，
故平行四边形的面积为
．
故答案为：
．
点评：本小题主要考查梯形与平行四边形的有关知识，以及分析问题和解决问题的能力，以及转化与化归的思想方法．本题的切入点是求梯形的内角，如何由已知分析出该点，是解题的关键．
解答：解：设等腰梯形的底角为θ，
则由图可知，θ+θ+θ=180°，即θ=60°．
由AD=CD=1知，
AB=CD+2AD•cos60°=2，
故梯形的面积为
=，故平行四边形的面积为
．故答案为：
．点评：本小题主要考查梯形与平行四边形的有关知识，以及分析问题和解决问题的能力，以及转化与化归的思想方法．本题的切入点是求梯形的内角，如何由已知分析出该点，是解题的关键．
练习册系列答案
相关题目
如图，四边形ABCD与A′ABB′都是边长为a的正方形，点E是A′A的中点，A′A⊥平面ABCD．
如图，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA=AB=
如图，四边形ABCD为矩形，且AD=2，AB=1，PA⊥平面ABCD，PA=1，E为BC的中点．
如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD
如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=