题目内容
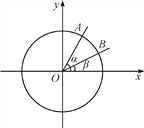
【题目】如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于A，B两点，已知A，B的横坐标分别为
，
.求：
（1）tan(α＋β)的值；
（2）α＋2β的大小．
【答案】(1)－3;(2) α＋2β＝
.
【解析】试题分析：（1）根据题意，由三角函数的定义可得
与
的值，进而可得出
与
的值，从而可求
与
的值就，结合两角和正切公式可得答案；（2）由两角和的正切公式，可得出
的值，再根据
的取值范围，可得出
的取值范围，进而可得出的值.
试题解析：15．解：（1）∵
，从而
．
又∵
，∴
． …
利用同角三角函数的基本关系可得sin2（α﹣β）+cos2（α﹣β）=1，且
，
解得 由条件得cosα＝
，cosβ＝
.
∵ α，β为锐角，
∴ sinα＝
＝
，sinβ＝
＝
.
因此tanα＝
＝7，tanβ＝
＝
.
(1) tan(αβ)＝
＝
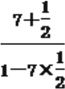＝－3.
(2) ∵ tan2β＝
＝
＝
，
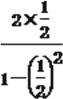∴ tan(α＋2β)＝
＝
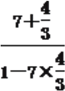＝－1.
∵ α，β为锐角，∴ 0<α＋2β<
，∴ α＋2β＝
练习册系列答案
相关题目
【题目】为了了解初三学生女生身高情况，某中学对初三女生身高进行了一次测量，所得数据整理后列出了频率分布表如下：
组 别 | 频数 | 频率 |
145．5～149．5 | 1 | 0．02 |
149．5～153．5 | 4 | 0．08 |
153．5～157．5 | 20 | 0．40 |
157．5～161．5 | 15 | 0．30 |
161．5～165．5 | 8 | 0．16 |
165．5～169．5 | m | n |
合 计 | M | N |
（1）求出表中
所表示的数分别是多少？
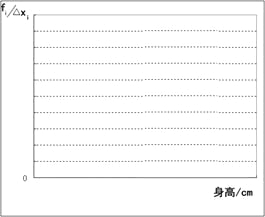
（2）画出频率分布直方图．
（3）全体女生中身高在哪组范围内的人数最多？由直方图确定此组数据中位数是多少？
