题目内容
已知椭圆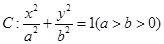 的离心率
的离心率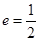 ,且椭圆过点
,且椭圆过点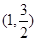 .
.
(1)求椭圆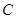 的方程;
的方程;
(2)若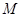 为椭圆
为椭圆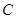 上的动点,
上的动点,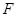 为椭圆的右焦点,以
为椭圆的右焦点,以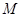 为圆心,
为圆心,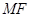 长为半径作圆
长为半径作圆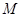 ,过点
,过点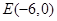 作圆
作圆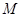 的两条切线
的两条切线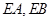 ,(
,(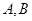 为切点),求点
为切点),求点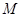 的坐标,使得四边形
的坐标,使得四边形 的面积最大.]
的面积最大.]
【答案】
(1)依题意得,
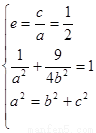 ………………………………3分
………………………………3分
解得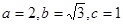 ,
,
所以椭圆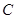 的方程为
的方程为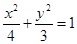 .
………………………………4分
.
………………………………4分
(2)设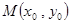 ,圆
,圆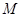 :
: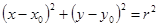 ,
,
其中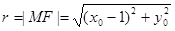
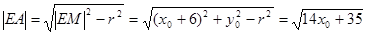 ,
,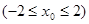 ……6分
……6分
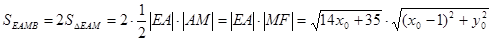 ……7分
……7分
又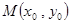 在椭圆
在椭圆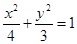 上,
上,
则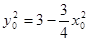
所以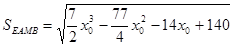 ,
,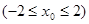 ………………………8分
………………………8分
令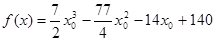 ,
,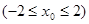
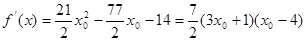 ,
,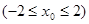 …………………9分
…………………9分
当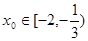 时,
时,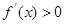 ,当
,当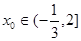 时,
时,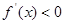 …………………10分
…………………10分
所以当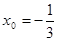 时,
时,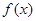 有最大值,
有最大值,
即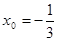 时,四边形
时,四边形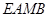 面积取得最大值…11分
面积取得最大值…11分
此时点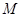 的坐标为
的坐标为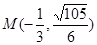 或
或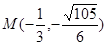 …………………………12分
…………………………12分
【解析】略

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 的离心率
的离心率 ,且右焦点F到左准线的距离为3.
,且右焦点F到左准线的距离为3. ,求p的最大值.
,求p的最大值.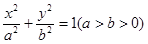 的离心率为
的离心率为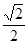 ,且过点
,且过点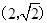 .
.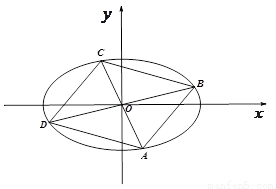
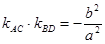 ,
,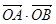 的最值.
的最值.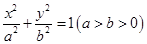 的离心率
的离心率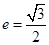 ,且短半轴
,且短半轴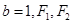 为其左右焦点,
为其左右焦点,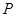 是椭圆上动点.
是椭圆上动点.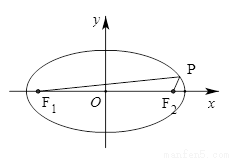
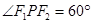 时,求
时,求 面积;
面积;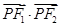 取值范围.
取值范围.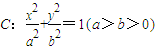 的离心率
的离心率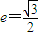 ,且过点
,且过点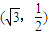 .
.