题目内容
若函数f(x)=(1+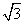 tanx)cosx,0≤x<
tanx)cosx,0≤x< ,则f(x)的最大值为( )
,则f(x)的最大值为( )
A.1 B.2
C.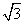 +1 D.
+1 D.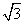 +2
+2
B
[解析] f(x)=(1+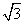 tanx)cosx
tanx)cosx
=cosx+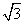 sinx=2sin
sinx=2sin ,
,
∵
∴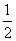 ≤sin
≤sin ≤1,∴f(x)的最大值为2.
≤1,∴f(x)的最大值为2.

练习册系列答案
相关题目
题目内容
若函数f(x)=(1+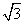 tanx)cosx,0≤x<
tanx)cosx,0≤x< ,则f(x)的最大值为( )
,则f(x)的最大值为( )
A.1 B.2
C.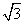 +1 D.
+1 D.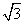 +2
+2
B
[解析] f(x)=(1+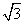 tanx)cosx
tanx)cosx
=cosx+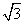 sinx=2sin
sinx=2sin ,
,
∵
∴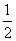 ≤sin
≤sin ≤1,∴f(x)的最大值为2.
≤1,∴f(x)的最大值为2.
