题目内容
已知 =ksinθ•
=ksinθ• +(2-cosθ)•
+(2-cosθ)• ,
, =
=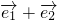 ,且
,且 ∥
∥ ,
, 与
与 不共线,θ∈(0,π).
不共线,θ∈(0,π).
(1)求k与θ的关系;
(2)求k=f(θ)的最小值.
解:(1)∵ ,∴
,∴
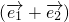 ,
,
∴ ∴k•sinθ=2-cosθ,
∴k•sinθ=2-cosθ,
 .
.
(2) =
=
= .
.
又∵θ∈(0,π),∴ .
.
∴
(当且仅当 ,即
,即 时取等号)
时取等号)
分析:(1)利用向量共线的充要条件列出等式,分离出k.
(2)利用三角函数的二倍角的正弦、余弦公式化简k的函数解析式;利用基本不等式求出最值,注意检验等号何时取得.
点评:本题考查向量共线的充要条件、考查三角函数的二倍角公式、考查利用基本不等式求函数的最值需满足的条件是:一正、二定、三相等.
 ,∴
,∴
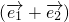 ,
,∴
 ∴k•sinθ=2-cosθ,
∴k•sinθ=2-cosθ, .
.(2)
 =
=
=
 .
.又∵θ∈(0,π),∴
 .
.∴

(当且仅当
 ,即
,即 时取等号)
时取等号)分析:(1)利用向量共线的充要条件列出等式,分离出k.
(2)利用三角函数的二倍角的正弦、余弦公式化简k的函数解析式;利用基本不等式求出最值,注意检验等号何时取得.
点评:本题考查向量共线的充要条件、考查三角函数的二倍角公式、考查利用基本不等式求函数的最值需满足的条件是:一正、二定、三相等.

练习册系列答案
相关题目
 =ksinθ•
=ksinθ•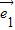 +(2-cosθ)•
+(2-cosθ)• ,
,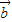 =
=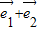 ,且
,且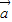 ∥
∥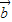 ,
,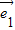 与
与 不共线,θ∈(0,π).
不共线,θ∈(0,π).