题目内容
10. 某班同学利用春节进行社会实践,对本地[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图.
某班同学利用春节进行社会实践,对本地[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图.| 序号 | 分组 | 本组“低碳族”的人数 | “低碳族”人数在本组中所占的比例 |
| 1 | [25,30) | 120 | 0.6 |
| 2 | [30,35) | 195 | p |
| 3 | [35,40) | 100 | 0.5 |
| 4 | [40,45) | a | 0.4 |
| 5 | [45,50) | 30 | 0.3 |
| 6 | [50,55] | 15 | 0.3 |
(二)各年龄段人数频率分布直方图:
(Ⅰ)在答题卡给定的坐标系中补全频率分布直方图,并求出n、p、a的值;
(Ⅱ)从[40,50]岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动.若将这6个人通过抽签分成甲、乙两组,每组的人数相同,求[45,50]岁中被抽取的人恰好又分在同一组的概率;
(Ⅲ)根据所得各年龄段人数频率分布直方图,估计在本地[25,55]岁的人群中“低碳族”年龄的中位数.
分析 (I)根据频率分步直方图的面积是这组数据的频率,做出频率,除以组距得到高,画出频率分步直方图的剩余部分,根据频率,频数和样本容量之间的关系,做出n、a、p的值.
(II)根据分层抽样方法做出两个部分的人数,列举出所有试验发生包含的事件和满足条件的事件,根据等可能事件的概率公式,得到结果;
(Ⅲ)根据在频率分布直方图中,中位数是所有小长方形的面积相等的分界线,可得答案.
解答 解:(Ⅰ)∵第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,
∴高为$\frac{0.3}{5}$=0.06.
频率直方图如下: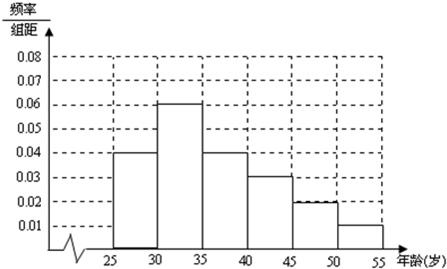
第一组的人数为$\frac{120}{0.6}$=200,频率为0.04×5=0.2,
∴n=$\frac{200}{0.2}$=1000.
由题可知,第二组的频率为0.3,
∴第二组的人数为1000×0.3=300,
∴p=$\frac{195}{300}$=0.65.
第四组的频率为0.03×5=0.15,
∴第四组的人数为1000×0.15=150,
∴a=150×0.4=60.
(Ⅱ)∵[40,45)岁年龄段的“低碳族”与[45,50)岁年龄段的“低碳族”的比值为60:30=2:1,
所以采用分层抽样法抽取6人,[40,45)岁中有4人,[45,50)岁中有2人.
设[40,45)岁中的4人为a、b、c、d,[45,50)岁中的2人为m、n,
将这6个人通过抽签分成甲、乙两组,每组的人数相同,共有$\frac{{C}_{6}^{3}}{2}$=10种不同的分法;
以a为研究对象,与a同组有:
(b,c)、(b,d)、(b,m)、(b,n)、(c,d)、
(c,m)、(c,n)、(d,m)、(d,n)、(m,n),
其中[45,50]岁中被抽取的人恰好又分在同一组的有:
(b,c)、(b,d)、(c,d)、(m,n)4种,
故[45,50]岁中被抽取的人恰好又分在同一组的概率P=$\frac{4}{10}$=$\frac{2}{5}$
(Ⅲ)∵前两组的累积频率5×0.04+5×0.06=0.5,
所以面积相等的分界线为35,
即中位数为35.
点评 本题考查频率分步直方图,考查频数,频率和样本容量之间的关系,考查等可能事件的概率,考查利用列举法来得到题目要求的事件数,本题是一个概率与统计的综合题目

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{π}{2}$ | B. | -$\frac{π}{2}$ | C. | $\frac{2}{π}$ | D. | -$\frac{2}{π}$ |
 如图是一个空间几何体的三视图,根据图中尺寸(单位:cm),可知几何体的表面积是( )
如图是一个空间几何体的三视图,根据图中尺寸(单位:cm),可知几何体的表面积是( )| A. | 18+2$\sqrt{3}$cm2 | B. | $\frac{{21\sqrt{3}}}{2}$cm2 | C. | 18+$\sqrt{3}$cm2 | D. | 6+2$\sqrt{3}$cm2 |
| A. | y=x3 | B. | y=$\root{3}{x}$ | C. | y=log3x | D. | y=($\frac{1}{3}$)x |
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{5}{3}$ | D. | $-\frac{1}{2}$ |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
