题目内容
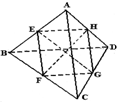空间四边形ABCD中，E、F、G、H顺次为边AB、BC、CD、DA的重点，且EG=3，FH=4，则AC2+BD2=50
50
．分析：根据平行四边形对角线的平方和等于四边的平方和，可得答案．
解答：解：∵点E，F，G，H分别为四边形ABCD的边AB，BC，CD，DA的中点，
∴HG、GF、FE、EH分别为△ADC、△BDC、△ABC、△ABD的中位线．
EG=3，FH=4，
∴EF=HG=
AC；
HE=FG=
×BD，
AC2+BD2=4（FG2+FE2）=2（GF2+EH2+EF2+HG2）=2（FH2+GE2）=50
故答案为：50．
解：∵点E，F，G，H分别为四边形ABCD的边AB，BC，CD，DA的中点，∴HG、GF、FE、EH分别为△ADC、△BDC、△ABC、△ABD的中位线．
EG=3，FH=4，
∴EF=HG=
| 1 |
| 2 |
HE=FG=
| 1 |
| 2 |
AC2+BD2=4（FG2+FE2）=2（GF2+EH2+EF2+HG2）=2（FH2+GE2）=50
故答案为：50．
点评：三角形中位线性质应用比较广泛，尤其是在三角形、四边形方面起着非常重要作用，本题解题的关键是将四边形分为四个三角形，然后利用中位线定理解答
练习册系列答案
相关题目
如图，已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点．
如图，空间四边形ABCD中，AB、BC、CD的中点分别是P、Q、R，且