题目内容
过椭圆C：
+y2=1的右焦点，作直线l交椭圆于M、N两点，且M、N到椭圆右准线的距离之和为
，求直线l的方程.
解析：由已知得a=2,c=,则其右焦点为F(,0)，右准线为x=
.
设M、N到右准线的距离为d1、d2,M(x1,y1),N(x2,y2),则d1+d2=
-x1+
-x2=
-(x1+x2).
由条件知d1+d2=
,∴x1+x2=
.
又当直线l的斜率不存在时，直线方程为x=3，此时M、N到x=
的距离之和为
，不合题意.故直线l的斜率存在.
设l的方程为y=k(x-
).
由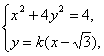
得(4k2+1)x2-8
k2x+12k2-4=0.
∴x1+x2=
.解
,得k=±
.
故所求直线的方程为y=±
(x-
).
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
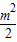=0，椭圆C：
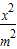+y2=1，F1、F2分别为椭圆C的左、右焦点．
=0，椭圆C：
+y2=1，F1、F2分别为椭圆C的左、右焦点．
+y2=1(a＞1)中心O的直线与椭圆C的左准线交于点M，与椭圆C交于点P，过点P与左焦点F1(-c，0)的直线l：x=my-c交椭圆C于另一点Q.
=且M的纵坐标为
时，求椭圆C的方程；
且椭圆C的离心率在(
)变化时,求实数m的取值范围.
+y2=1(a＞1)中心O的直线与椭圆C的左准线交于点M，与椭圆C交于点P，过点P与左焦点F1(-c，0)的直线l：x=my-c交椭圆C于另一点Q．
且M的纵坐标为
时，求椭圆C的方程；
，且
时，求m的值．