题目内容
已知双曲线C: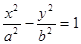 离心率是
离心率是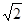 ,过点
,过点 ,且右支上的弦
,且右支上的弦 过右焦点
过右焦点 .
.
(1)求双曲线C的方程;
(2)求弦 的中点
的中点 的轨迹E的方程;
的轨迹E的方程;
(3)是否存在以 为直径的圆过原点O?,若存在,求出直线
为直径的圆过原点O?,若存在,求出直线 的斜率k 的值.若不存在,则说明理由.
的斜率k 的值.若不存在,则说明理由.
(1) ;(2)
;(2)  ,(
,( ;(3) 这样的圆不存在.
;(3) 这样的圆不存在.
解析试题分析:(1)由已知条件双曲线C: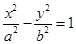 离心率是
离心率是 ,过点
,过点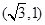 ,由此能求出双曲线C的标准方程.(2)设M(x,y),
,由此能求出双曲线C的标准方程.(2)设M(x,y),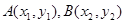 ,将
,将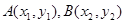 代入椭圆方程,再利用“点差法”即可求出M的轨迹方程;(3)设
代入椭圆方程,再利用“点差法”即可求出M的轨迹方程;(3)设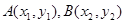 ,
, 由已知
由已知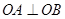 得:
得: ,将
,将 联立,得
联立,得
 ,将
,将
 代入
代入 得
得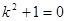 ,即可得出结论.
,即可得出结论.
(1).
(2) ,(
,( )-------6分 注:没有
)-------6分 注:没有 扣1分
扣1分
(3)假设存在,设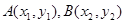 ,
,
由已知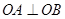 得:
得:
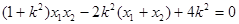 ①
①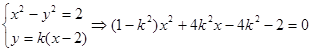
所以
 ②
②
联立①②得: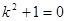 无解
无解
所以这样的圆不存在. 12分
考点:1.椭圆方程;2.直线与椭圆的位置关系.

练习册系列答案
相关题目
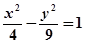 ,F1,F2是其两个焦点,点M在双曲线上.
,F1,F2是其两个焦点,点M在双曲线上.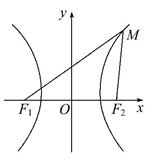
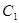 的圆心在坐标原点
的圆心在坐标原点 ,且恰好与直线
,且恰好与直线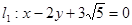 相切,设点A为圆上一动点,
相切,设点A为圆上一动点,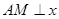 轴于点
轴于点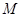 ,且动点
,且动点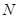 满足
满足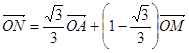 ,设动点
,设动点
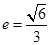 ,过
,过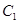 的左焦点
的左焦点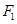 的直线
的直线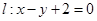 被圆
被圆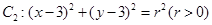 截得的弦长为
截得的弦长为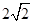 .
. ,在圆
,在圆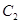 上是否存在点
上是否存在点 ,满足
,满足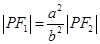 ,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由. :
: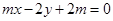
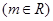 和椭圆
和椭圆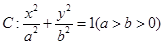 ,椭圆C的离心率为
,椭圆C的离心率为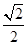 ,连结椭圆的四个顶点形成四边形的面积为
,连结椭圆的四个顶点形成四边形的面积为 .
.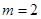 时,设直线
时,设直线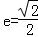 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.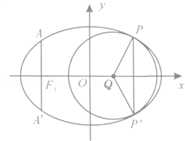
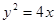 的顶点作射线
的顶点作射线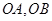 与抛物线交于
与抛物线交于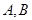 ,若
,若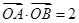 ,求证:直线
,求证:直线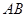 过定点.
过定点. :
: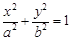 (
(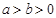 )过点
)过点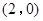 ,且椭圆
,且椭圆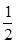 .
.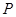 在直线
在直线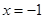 上,过
上,过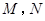 两点,且
两点,且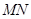 中点,再过
中点,再过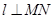 .求直线
.求直线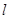 是否恒过定点,如果是则求出该定点的坐标,不是请说明理由。
是否恒过定点,如果是则求出该定点的坐标,不是请说明理由。 的长轴长为
的长轴长为 ,离心率为
,离心率为 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点 ,且与直线
,且与直线 相切.
相切. 的方程;(ⅱ)求动圆圆心轨迹
的方程;(ⅱ)求动圆圆心轨迹 的方程;
的方程; ,满足
,满足 与
与 共线,
共线, 与
与 共线,且
共线,且 ,求四边形
,求四边形 面积的最小值.
面积的最小值.