题目内容
如图,设有双曲线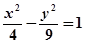 ,F1,F2是其两个焦点,点M在双曲线上.
,F1,F2是其两个焦点,点M在双曲线上.
(1)若∠F1MF2=90°,求△F1MF2的面积;
(2)若∠F1MF2=60°,△F1MF2的面积是多少?若∠F1MF2=120°,△F1MF2的面积又是多少?
(3)观察以上计算结果,你能看出随∠F1MF2的变化,△F1MF2的面积将怎样变化吗?试证明你的结论.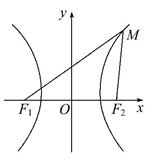
(1) 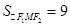 ; (2)
; (2) 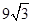 ,
,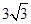 ; (3) θ增大时面积变小,证明过程见解析.
; (3) θ增大时面积变小,证明过程见解析.
解析试题分析:(1) 设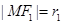 ,
,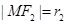 , 直角三角形△F1MF2中
, 直角三角形△F1MF2中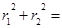
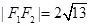 ,利用双曲线定义得
,利用双曲线定义得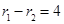 ,平方得
,平方得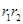 ,求得面积;(2) △F1MF2 中由余弦定理可得,|MF1|·|MF2|,由面积公式
,求得面积;(2) △F1MF2 中由余弦定理可得,|MF1|·|MF2|,由面积公式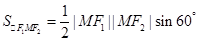 可得面积;(3) 由双曲线定义与余弦定理,可得面积与θ的关系
可得面积;(3) 由双曲线定义与余弦定理,可得面积与θ的关系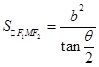 ,所以θ增大时面积变小.
,所以θ增大时面积变小.
解:(1)由双曲线方程知a=2,b=3,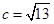 ,
,
设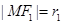 ,
,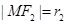 (
(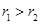 ).
).
由双曲线定义,有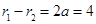 ,两边平方得,
,两边平方得,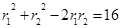 ,
,
即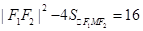 ,
,
也即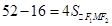 ,求得
,求得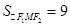 . 4分
. 4分
(2)若∠F1MF2=60°,在△MF1F2中,
由余弦定理得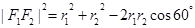 ,
,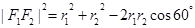 ,所以
,所以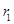
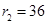 .
.
求得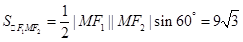 .
.
同理可求得若∠F1MF2=120°, 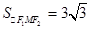 . 8分
. 8分
(3)由以上结果猜想,随着∠F1MF2的增大,△F1MF2的面积将减小.
证明如下:
令∠F1MF2=θ,则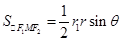 .
.
由双曲线定义及余弦定理,有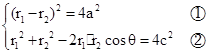
②-①得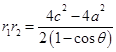 ,
,
所以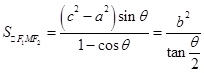 ,
,
因为0<θ<π,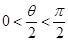 ,
,
在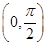 内,
内,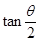 是增函数,
是增函数,
因此当θ增大时, 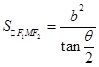 将减小. 12分
将减小. 12分
考点:双曲线的定义,余弦定理,三角形面积公式.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
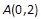 ,右焦点F与点
,右焦点F与点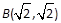 的距离为2。
的距离为2。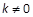 的直线
的直线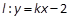 与椭圆相交于不同的两点M,N满足
与椭圆相交于不同的两点M,N满足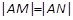 ,求直线l的方程。
,求直线l的方程。
 中,
中, 分别是椭圆
分别是椭圆 的左右焦点,顶点
的左右焦点,顶点 的坐标是
的坐标是 ,连接
,连接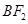 并延长交椭圆于点
并延长交椭圆于点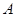 ,过点
,过点 轴的垂线交椭圆于另一点
轴的垂线交椭圆于另一点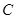 ,连接
,连接 .
.
 ,且
,且 ,求椭圆的方程;
,求椭圆的方程;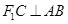 ,求椭圆离心率
,求椭圆离心率 的值.
的值.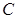 由上半椭圆
由上半椭圆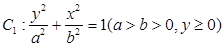 和部分抛物线
和部分抛物线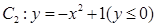 连接而成,
连接而成, 的公共点为
的公共点为 ,其中
,其中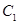 的离心率为
的离心率为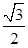 .
.
 的值;
的值;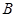 的直线
的直线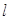 与
与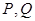 (均异于点
(均异于点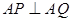 ,求直线
,求直线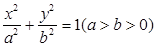 的左、右焦点分别为
的左、右焦点分别为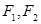 ,点
,点 在椭圆上,
在椭圆上,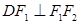 ,
,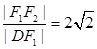 ,
,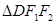 的面积为
的面积为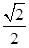 .
. 轴上的圆与椭圆在
轴上的圆与椭圆在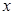 轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径..
轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径..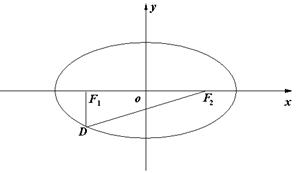
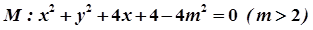 上任意一点,点N的坐标为(2,0),线段NP的垂直平分线交直线MP于点Q,当点P在圆M上运动时,点Q的轨迹为C.
上任意一点,点N的坐标为(2,0),线段NP的垂直平分线交直线MP于点Q,当点P在圆M上运动时,点Q的轨迹为C.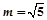 时,在x轴上是否存在一定点E,使得对曲线C的任意一条过E的弦AB,
时,在x轴上是否存在一定点E,使得对曲线C的任意一条过E的弦AB,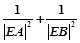 为定值?若存在,求出定点和定值;若不存在,请说明理由.
为定值?若存在,求出定点和定值;若不存在,请说明理由.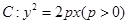 的焦点
的焦点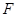 到准线的距离为
到准线的距离为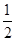 .过点
.过点
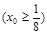
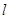 交抛物线
交抛物线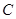 与
与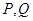 两点(
两点( 在第一象限内).
在第一象限内). 与焦点
与焦点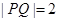 .求直线
.求直线 关于
关于 轴的对称点为
轴的对称点为 .直线
.直线 交
交 . 且
. 且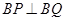 .求点
.求点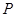 是椭圆
是椭圆 上任一点,点
上任一点,点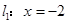 的距离为
的距离为 ,到点
,到点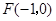 的距离为
的距离为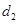 ,且
,且 .直线
.直线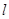 与椭圆
与椭圆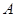 、
、 (
( 轴上方) ,且
轴上方) ,且 .
.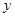 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线 如何变化,直线
如何变化,直线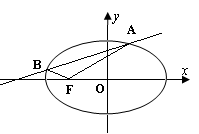
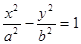 离心率是
离心率是 ,过点
,过点 ,且右支上的弦
,且右支上的弦 过右焦点
过右焦点 .
. 的轨迹E的方程;
的轨迹E的方程;