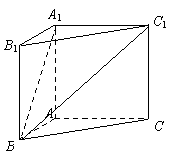
题目内容
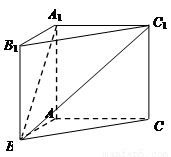
在直三棱柱![]() 中,
中,![]() ,
,![]() ,且异面直线
,且异面直线![]() 与
与![]() 所成的角等于
所成的角等于![]() ,设
,设![]() .(1)求
.(1)求![]() 的值;(2)求平面
的值;(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的大小.
所成的锐二面角的大小.

解法一:(1)![]()
![]() ,
,
![]()
![]() 就是异面直线
就是异面直线![]() 与
与![]() 所成的角,
所成的角,
即![]() ,……(2分)
,……(2分)
连接![]() ,又
,又![]() ,则
,则![]()
![]()
![]() 为等边三角形,……………………………3分
为等边三角形,……………………………3分
由![]() ,
,![]()
![]() ,
,
![]()
![]() ;………5分
;………5分
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
![]() ,
,![]()
![]() 平面
平面![]()
![]()
![]() ………………7分
………………7分
又![]() ,所以
,所以![]() 平面
平面![]() ,即
,即![]() ,
,
所以![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成的锐二面角的平面角。…………9分
所成的锐二面角的平面角。…………9分
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]() ,…………………………11分
,…………………………11分
因此平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() 。…………12分
。…………12分
说明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,…………同样给分(也给10分)
,…………同样给分(也给10分)
解法二:(1)建立如图坐标系,于是![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() )
)

![]() ,
,![]() ,
,![]()
![]() …………3分
…………3分
由于异面直线![]() 与
与![]() 所成的角
所成的角![]() ,
,
所以![]() 与
与![]() 的夹角为
的夹角为![]()
即![]()
![]() ………5分
………5分
(2)设向量![]() 且
且![]() 平面
平面![]()
于是![]() 且
且![]() ,即
,即![]() 且
且![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,不妨设
,不妨设![]() ……7分
……7分
同理得![]() ,使
,使![]() 平面
平面![]() ,(9分)
,(9分)
设![]() 与
与![]() 的夹角为
的夹角为![]() ,所以依
,所以依![]() ,
,
![]() ,………………11分
,………………11分
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
因此平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() 。…………12分
。…………12分
说明:或者取![]() 的中点
的中点![]() ,连接
,连接![]() ,于是
,于是![]() 显然
显然![]() 平面
平面![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 且异面直线
且异面直线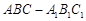 中,
中,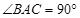 ,
,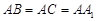 ,且
,且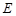 是
是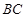 中点.
中点.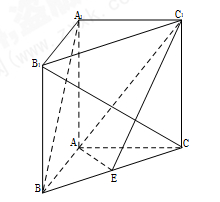
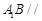 平面
平面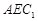 ;
;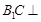 平面
平面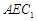 .
. 中,
中, ,
, ,且异面直线
,且异面直线 与
与 所成的角等于
所成的角等于 ,设
,设
 的值;
的值; 到平面
到平面 的距离。
的距离。
 中,
中,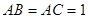 ,
,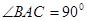 ,且异面直线
,且异面直线 与
与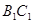 所成的角等于
所成的角等于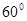 ,设
,设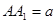 .
.
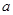 的值;
的值;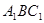 与平面
与平面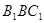 所成的锐二面角的大小
所成的锐二面角的大小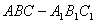 中,
中,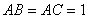 ,
,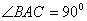 ,且异面直线
,且异面直线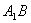 与
与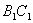 所成的角等于
所成的角等于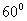 ,设
,设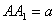 .
.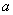 的值;
的值; 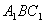 与平面
与平面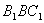 所成的锐二面角的大小.
所成的锐二面角的大小.