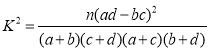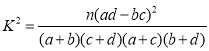题目内容
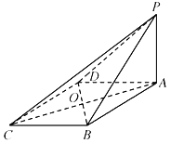
【题目】如图1,四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 为
为![]() 的中点,以
的中点,以![]() 为折痕将
为折痕将![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如图2.
,如图2.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由题意可证得![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]() 可证;
可证;
(2)解法一:利用等体积法由![]() 可求出点
可求出点![]() 到平面
到平面![]() 的距离;解法二:由条件知点
的距离;解法二:由条件知点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,过点
的距离,过点![]() 作
作![]() 的垂线,垂足
的垂线,垂足![]() ,证明
,证明![]() 平面
平面![]() ,计算出
,计算出![]() 即可.
即可.
解法一:(1)依题意知,因为![]() ,所以
,所以![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() .
.
由已知,![]() 是等边三角形,且
是等边三角形,且![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
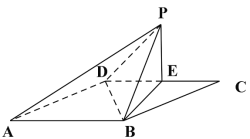
(2)在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() .
.
由(1)知,![]() 平面
平面![]() ,且
,且![]() ,
,
所以三棱锥![]() 的体积
的体积![]() .
.
在![]() 中,
中,![]() ,
,![]() ,得
,得![]() ,
,
由(1)知,![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() ,
,
设点![]() 到平面
到平面![]() 的距离
的距离![]() ,
,
则三棱锥![]() 的体积
的体积![]() ,得
,得![]() .
.
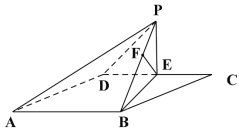
解法二:(1)同解法一;
(2)因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离.
的距离.
过点![]() 作
作![]() 的垂线,垂足
的垂线,垂足![]() ,即
,即![]() .
.
由(1)知,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
由(1)知,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,得
,得![]() .
.
又![]() ,所以
,所以![]() .
.
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某地方政府召开全面展开新旧动能转换重大工程动员大会,动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前、后生产的大量产品中各抽取了200件作为样本,检测一项质量指标值.若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.如图所示的是设备改造前样本的频率分布直方图.
内的产品视为合格品,否则为不合格品.如图所示的是设备改造前样本的频率分布直方图.
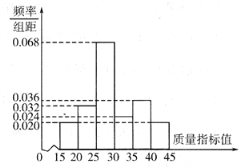
(1)若设备改造后样本的该项质量指标值服从正态分布![]() ,求改造后样本中不合格品的件数;
,求改造后样本中不合格品的件数;
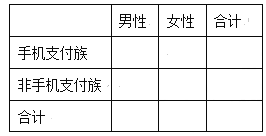
(2)完成下面2×2列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量标值与设备改造有关.
0 | 设备改造前 | 设备改造后 | 合计 |
合格品件数 | |||
不合格品件数 | |||
合计 |
附参考公式和数据:
若![]() ,则
,则![]() ,
,![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 |