Question

袋中有红、黄、白3种颜色的球各一只,从中每次任取1只,有放回地抽取3次,求:

(1)3只全是红球的概率;

(2)3只颜色全相同的概率;

(3)3只颜色不全相同的概率;

(4)3只颜色全不相同的概率.

Answer 1

解析：利用互斥事件和对立事件概率公式求概率.?

(1)记“3只全是红球”的事件为A,从袋中有放回地抽取3次,每次取1只,共会出现3×3×3=27种等可能的结果,其中3只全是红球的只有一种,故事件A的概率为P(A)=.? 

(2)“3只颜色全相同”只可能有三种情况,“三只全是红球”记为事件A,“三只全是黄球”记为事件B,“三只全是白球”记为事件C,由于它们不能同时发生,是彼此互斥事件,由(1)得P(B)=P(C)=P(A)= ,所以P(A+B+C)=P(A)+P(B)+P(C)=.?

(3)3只颜色不全相同的情况较多,可以是两只黄球一只白球,也可以是两只白球一只红球或是三种颜色各一只.考虑进来比较麻烦,现记“3只颜色不全相同”为事件D,则事件D为“3只颜色全相同”,显然用对立事件的概率来求比较方便,所以P(D)=1-P()=1-=.?

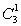
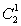
(4)要使3只颜色全不相同,只可能是红、黄、白球各一只,要分三次抽取,故3次抽到红、黄、白球各一只的可能结果为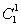=6种或A³₃=6种,故三只颜色全不相同的概率为P(E)=.

答案：(1);(2) ;(3) ;(4).