题目内容
已知函数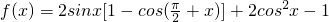
(1)设ω>0为常数,若函数y=f(ωx)在区间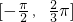 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;
(2)设集合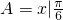 ≤x≤
≤x≤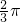 ,B=x||f(x)-m|<2,若A∪B=B,求实数m的取值范围.
,B=x||f(x)-m|<2,若A∪B=B,求实数m的取值范围.
解:f(x)=2sinx+2sin2x+2cos2x-1=2sinx+1
(1)y=f(ωx)=2sinωx+1在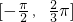 上增函数
上增函数
∵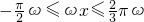
∴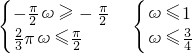
∴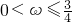
(2)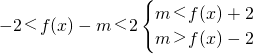
又A∪B=B,∴A⊆B
∴对于任意 ,不等式
,不等式 恒成立
恒成立
而 且最大值f(x)max=3,最小值f(x)min=2
且最大值f(x)max=3,最小值f(x)min=2
∴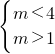
∴1<m<4
实数m的取值范围1<m<4
分析:(1)利用三角函数的平方关系及二倍角公式化简三角函数,再由函数y=f(ωx)在区间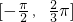 上是增函数列出关于ω的不等关系,解这即得ω的取值范围;
上是增函数列出关于ω的不等关系,解这即得ω的取值范围;
(2)利用A∪B=B得出集合A是集合B的子集,再化简集合B,最后转化为不等式 恒成立问题,从而实数m的取值范围即可.
恒成立问题,从而实数m的取值范围即可.
点评:本小题主要考查函数二倍角的余弦、三角函数中的恒等变换应用、并集及其运算、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
(1)y=f(ωx)=2sinωx+1在
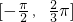 上增函数
上增函数∵
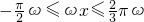
∴
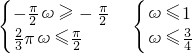
∴
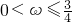
(2)
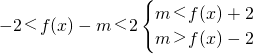
又A∪B=B,∴A⊆B
∴对于任意
 ,不等式
,不等式 恒成立
恒成立而
 且最大值f(x)max=3,最小值f(x)min=2
且最大值f(x)max=3,最小值f(x)min=2∴
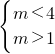
∴1<m<4
实数m的取值范围1<m<4
分析:(1)利用三角函数的平方关系及二倍角公式化简三角函数,再由函数y=f(ωx)在区间
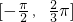 上是增函数列出关于ω的不等关系,解这即得ω的取值范围;
上是增函数列出关于ω的不等关系,解这即得ω的取值范围;(2)利用A∪B=B得出集合A是集合B的子集,再化简集合B,最后转化为不等式
 恒成立问题,从而实数m的取值范围即可.
恒成立问题,从而实数m的取值范围即可.点评:本小题主要考查函数二倍角的余弦、三角函数中的恒等变换应用、并集及其运算、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
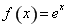
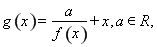
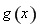
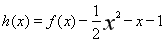
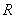
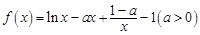 .
.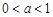 ,试讨论
,试讨论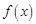 单调性;
单调性;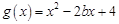 ,当
,当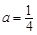 时,若
时,若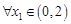 ,存在
,存在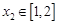 ,使
,使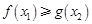 ,求实数
,求实数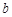 的
的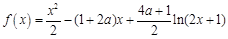 .
.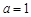 时,求函数
时,求函数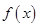 极大值和极小值;
极大值和极小值;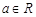 时讨论函数
时讨论函数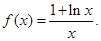
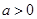 ,若函数在区间
,若函数在区间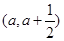 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;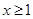 时,不等式
时,不等式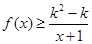 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。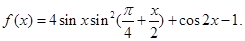
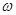 >0为常数,若
>0为常数,若 上是增函数,求
上是增函数,求 若A
若A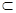 B恒成立,求实数
B恒成立,求实数 的取值范围
的取值范围