题目内容
4.集合A={(x,y)|y=|x|},集合B={(x,y)|y>0,x∈R},则下列说法正确的是( )| A. | A⊆B | B. | B⊆A | ||
| C. | A∩B=∅ | D. | 集合A、B间没有包含关系 |
分析 可以看出集合A表示直线y=x和y=-x在x轴上方的部分,并且包含原点,而集合B表示x轴上面的点形成的集合,不包含原点,这便可得出集合A,B没有包含关系.
解答 解:A={(x,y)|y≥0,x∈R,且y=|x|};
∴(0,0)∈A,而(0,0)∉B;
(0,1)∈B,而(0,1)∉A;
∴集合A,B间没有包含关系.
故选:D.
点评 考查描述法表示集合,元素与集合的关系,用有序数对表示点,以及两集合的包含关系的确定.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
12.已知f(x),g(x)都是R上的奇函数,f(x)>0的解集为(a2,b),g(x)>0的解集为($\frac{{a}^{2}}{2}$,$\frac{b}{2}$),且a2<$\frac{b}{2}$,则f(x)•g(x)>0的解集为( )
| A. | (-$\frac{b}{2}$,-a2)∪(a2,$\frac{b}{2}$) | B. | (-$\frac{b}{2}$,a2)∪(-a2,$\frac{b}{2}$) | C. | (-$\frac{b}{2}$,-a2)∪(a2,b) | D. | (-b,-a2)∪(a2,$\frac{b}{2}$) |
19.函数f(x)是奇函数,且在(0,+∞)内是单调递增函数,若f(3)=0,则不等式xf(x)<0的解集是( )
| A. | (-3,0)∪(3,+∞) | B. | (-∞,-3)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(0,3) |
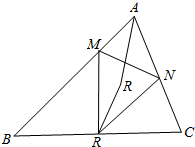 已知△ABC为锐角三角形,AB≠AC,以BC为直径的圆分别交边AB和AC于点M和N,记BC得中点为O,∠BAC的平分线和∠MON的平分线交于点R.证明:△BMR的外接圆和△CNR的外接圆有一个交点在BC上.
已知△ABC为锐角三角形,AB≠AC,以BC为直径的圆分别交边AB和AC于点M和N,记BC得中点为O,∠BAC的平分线和∠MON的平分线交于点R.证明:△BMR的外接圆和△CNR的外接圆有一个交点在BC上.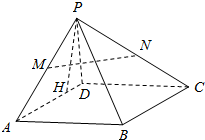 如图,四棱锥P-ABCD,底面ABCD为正方形,平面PAD⊥平面ABCD,PA=$\sqrt{3}$,PD=1,AD=2,PH⊥AD交AD于H.
如图,四棱锥P-ABCD,底面ABCD为正方形,平面PAD⊥平面ABCD,PA=$\sqrt{3}$,PD=1,AD=2,PH⊥AD交AD于H.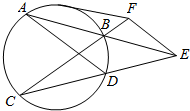 如图,已知圆的两条弦AB,CD,延长AB,CD交于圆外一点E,过E作AD的平行线交CB的延长线于F,过点F作圆的切线FG,G为切点.求证:
如图,已知圆的两条弦AB,CD,延长AB,CD交于圆外一点E,过E作AD的平行线交CB的延长线于F,过点F作圆的切线FG,G为切点.求证: