题目内容
若存在实数x∈[2,4],使x2-2x+5-m<0成立,则m的取值范围为
| A.(13,+∞) | B.(5,+∞) | C.(4,+∞) | D.(-∞,13) |
B
解析试题分析:因为,存在实数x∈[2,4],使x2-2x+5-m<0成立,所以存在实数x∈[2,4]使x2-2x+5< m,而x∈[2,4]时,x2-2x+5=(x-1)2+4最大值为13,最小值为5,故选B。
考点:本题主要考查二次函数的图象和性质,分离参数法解恒成立问题。
点评:典型题,恒成立或存在性问题,一般的通过分离参数,转化成求函数最值。本题主要考查二次函数在闭区间的最值求法。

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知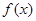 为定义在
为定义在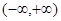 上的可导函数,且
上的可导函数,且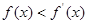 对于任意
对于任意 恒成立,则( )
恒成立,则( )
A.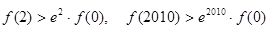 |
B.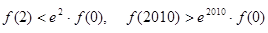 |
C.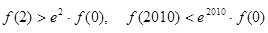 |
D.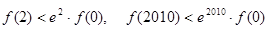 |
设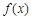 在
在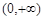 上是单调递增函数,当
上是单调递增函数,当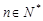 时,
时,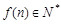 ,且
,且 ,则( )
,则( )
A.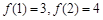 | B. |
C.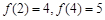  | D.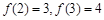 |
下列函数在区间[0, ]上是减函数的是
]上是减函数的是
| A.y="sin" x | B.y="cos" x | C.y="tan" x | D.y=2 |
函数f(x)=2x+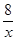 (x>0)有
(x>0)有
| A.最大值8 | B.最小值8 | C.最大值4 | D.最小值4 |
函数 的单调递减区间是 ( )
的单调递减区间是 ( )
A. | B. | C. | D. |
关于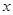 的方程
的方程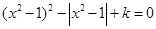 ,给出下列四个命题:
,给出下列四个命题:
①存在实数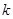 ,使得方程恰有2个不同实根; ②存在实数
,使得方程恰有2个不同实根; ②存在实数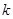 ,使得方程恰有4个不同实根;
,使得方程恰有4个不同实根;
③存在实数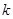 ,使得方程恰有5个不同实根; ④存在实数
,使得方程恰有5个不同实根; ④存在实数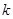 ,使得方程恰有8个不同实根;
,使得方程恰有8个不同实根;
其中假命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
函数 ( )
( )
A.是奇函数,且在 上是单调增函数 上是单调增函数 |
B.是奇函数,且在 上是单调减函数 上是单调减函数 |
C.是偶函数,且在 上是单调增函数 上是单调增函数 |
D.是偶函数,且在 上是单调减函数 上是单调减函数 |
已知函数 ,则该函数是 ( )
,则该函数是 ( )
A.偶函数,且单调递增  | B.偶函数,且单调递减 |
| C.奇函数,且单调递增 | D.奇函数,且单调递减 |