题目内容
 如下图所示,两射线OA与OB交于点O,下列5个向量中,
如下图所示,两射线OA与OB交于点O,下列5个向量中,
①2 ②
② ③
③ ④
④ ⑤
⑤
若以O为起点,终点落在阴影区域内(含边界)的向量有 个.
- A.1
- B.2
- C.3
- D.4
A
分析:根据平面向量基本定理,可得到 =t
=t +(1-t)
+(1-t) ,由M在阴影区域内可得实数r≥1使得
,由M在阴影区域内可得实数r≥1使得 =r
=r ,从而
,从而 =rt
=rt +r(1-t)
+r(1-t) ,根据 rt+r(1-t)=r≥1,r(1-t)≥0,得出结论.
,根据 rt+r(1-t)=r≥1,r(1-t)≥0,得出结论.
解答:设M在阴影区域内,则射线OM与线段AB有公共点,记为N,则存在实数t∈(0,1]使得 =t
=t +(1-t)
+(1-t) ,
,
且存在实数r≥1,使得 =r
=r ,从而
,从而 =rt
=rt +r(1-t)
+r(1-t) ,且 rt+r(1-t)=r≥1.
,且 rt+r(1-t)=r≥1.
又由于 0≤t≤1,故 r(1-t)≥0.
①中rt=2,r(1-t)=-1<0,rt+r(1-t)=r=1,满足r≥1但不满足r(1-t)≥0,故①不满足条件.
②中rt= ,r(1-t)=
,r(1-t)= ,rt+r(1-t)=r=
,rt+r(1-t)=r= ,故②满足条件.
,故②满足条件.
③中rt= ,r(1-t)=
,r(1-t)= ,rt+r(1-t)=r=
,rt+r(1-t)=r= ,不满足r≥1,故③不满足条件.
,不满足r≥1,故③不满足条件.
④中rt= ,(1-t)=
,(1-t)= ,rt+r(1-t)=r=
,rt+r(1-t)=r=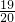 ,不满足r≥1,故④不满足条件.
,不满足r≥1,故④不满足条件.
⑤中rt= ,r(1-t)=-
,r(1-t)=- ,rt+r(1-t)=r=
,rt+r(1-t)=r=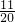 ,不满足r≥1,故⑤不满足条件.
,不满足r≥1,故⑤不满足条件.
综上,只有①满足条件,
故选:A.
点评:本题主要考查平面向量基本定理,向量数乘的运算及其几何意义,得到 =t
=t +(1-t)
+(1-t) ,是解题的关键.
,是解题的关键.
分析:根据平面向量基本定理,可得到
 =t
=t +(1-t)
+(1-t) ,由M在阴影区域内可得实数r≥1使得
,由M在阴影区域内可得实数r≥1使得 =r
=r ,从而
,从而 =rt
=rt +r(1-t)
+r(1-t) ,根据 rt+r(1-t)=r≥1,r(1-t)≥0,得出结论.
,根据 rt+r(1-t)=r≥1,r(1-t)≥0,得出结论.解答:设M在阴影区域内,则射线OM与线段AB有公共点,记为N,则存在实数t∈(0,1]使得
 =t
=t +(1-t)
+(1-t) ,
,且存在实数r≥1,使得
 =r
=r ,从而
,从而 =rt
=rt +r(1-t)
+r(1-t) ,且 rt+r(1-t)=r≥1.
,且 rt+r(1-t)=r≥1.又由于 0≤t≤1,故 r(1-t)≥0.
①中rt=2,r(1-t)=-1<0,rt+r(1-t)=r=1,满足r≥1但不满足r(1-t)≥0,故①不满足条件.
②中rt=
 ,r(1-t)=
,r(1-t)= ,rt+r(1-t)=r=
,rt+r(1-t)=r= ,故②满足条件.
,故②满足条件.③中rt=
 ,r(1-t)=
,r(1-t)= ,rt+r(1-t)=r=
,rt+r(1-t)=r= ,不满足r≥1,故③不满足条件.
,不满足r≥1,故③不满足条件.④中rt=
 ,(1-t)=
,(1-t)= ,rt+r(1-t)=r=
,rt+r(1-t)=r=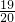 ,不满足r≥1,故④不满足条件.
,不满足r≥1,故④不满足条件.⑤中rt=
 ,r(1-t)=-
,r(1-t)=- ,rt+r(1-t)=r=
,rt+r(1-t)=r=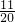 ,不满足r≥1,故⑤不满足条件.
,不满足r≥1,故⑤不满足条件.综上,只有①满足条件,
故选:A.
点评:本题主要考查平面向量基本定理,向量数乘的运算及其几何意义,得到
 =t
=t +(1-t)
+(1-t) ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目
 如下图所示,两射线OA与OB交于点O,下列5个向量中,
如下图所示,两射线OA与OB交于点O,下列5个向量中, ②
② ③
③ ④
④ ⑤
⑤

 ②
② ③
③ ④
④ ⑤
⑤
