题目内容
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面ABCD,侧棱
底面ABCD,侧棱![]() ,
,![]() ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中![]() ,
,![]() ,
,![]() ,O为AD中点.
,O为AD中点.
![]() 求直线PB与平面POC所成角的余弦值.
求直线PB与平面POC所成角的余弦值.
![]() 求B点到平面PCD的距离.
求B点到平面PCD的距离.
![]() 线段PD上是否存在一点Q,使得二面角
线段PD上是否存在一点Q,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

【答案】(1)![]() (2)
(2)![]() (3)存在,
(3)存在,![]()
【解析】
试题(1)易得![]() 平面
平面![]() ,所以
,所以![]() 即为所求.(2)由于
即为所求.(2)由于![]() ,从而
,从而![]() 平面
平面![]() ,所以可转化为求点
,所以可转化为求点![]() 到平面
到平面![]() .(3)假设存在,过Q作
.(3)假设存在,过Q作![]() ,垂足为
,垂足为![]() ,过
,过![]() 作
作![]() ,垂足为M,则
,垂足为M,则![]() 即为二面角
即为二面角![]() 的平面角.设
的平面角.设![]() ,利用
,利用![]() 求出
求出![]() ,若
,若![]() ,则存在,否则就不存在.
,则存在,否则就不存在.
试题解析:(1) 在△PAD中PA="PD," O为AD中点,所以PO⊥AD,
又侧面PAD⊥底面ABCD, 平面![]() 平面ABCD="AD,"
平面ABCD="AD,"![]() 平面PAD,
平面PAD,
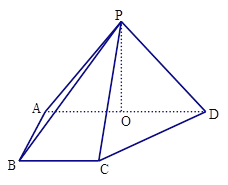
所以PO⊥平面ABCD.
又在直角梯形![]()
![]() 中,易得
中,易得![]()
![]() ;
;
所以以![]()
![]() 为坐标原点
为坐标原点![]() ,
,![]() 为
为![]()
![]() 轴,
轴,![]()
![]() 为
为![]()
![]() 轴,
轴,
![]() 为
为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]()
![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ;
;
![]() , 易证
, 易证![]() :
:![]() ,
,
所以![]()
![]() 平面
平面![]() 的法向量,
的法向量,
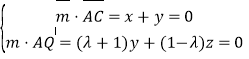
所以![]()
![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]()
(2)![]()
![]() ,设平面PDC的法向量为
,设平面PDC的法向量为![]() ,
,
则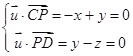 ,取
,取![]()
![]() 得
得![]()
![]() 点到平面
点到平面![]()
![]() 的距离
的距离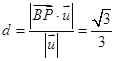
(3)假设存在,且设![]() .
.
因为![]()
所以![]() ,
,
设平面CAQ的法向量中![]() ,则
,则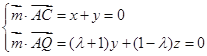
取![]() ,得
,得![]() .
.
平面CAD的一个法向量为![]() ,
,
因为二面角Q OC D的余弦值为![]() ,所以
,所以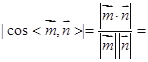
![]() .
.
整理化简得:![]() 或
或![]() (舍去),
(舍去),
所以存在,且![]()

练习册系列答案
相关题目