题目内容
已知直线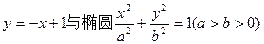 相交于
相交于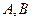 两点,且
两点,且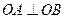 (其中O为坐标原点).
(其中O为坐标原点).
(1)若椭圆的离心率为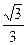 ,求椭圆的标准方程;(2)求证:不论
,求椭圆的标准方程;(2)求证:不论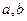 如何变化,椭圆恒过第一象限内的一个定点
如何变化,椭圆恒过第一象限内的一个定点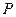 ,并求点
,并求点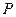 的坐标;(3)若椭圆的离心率
的坐标;(3)若椭圆的离心率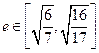 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.
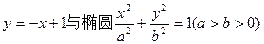 相交于
相交于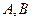 两点,且
两点,且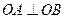 (其中O为坐标原点).
(其中O为坐标原点).(1)若椭圆的离心率为
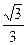 ,求椭圆的标准方程;(2)求证:不论
,求椭圆的标准方程;(2)求证:不论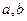 如何变化,椭圆恒过第一象限内的一个定点
如何变化,椭圆恒过第一象限内的一个定点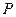 ,并求点
,并求点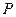 的坐标;(3)若椭圆的离心率
的坐标;(3)若椭圆的离心率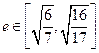 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.(1)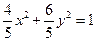 (2)略 (3)
(2)略 (3)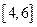
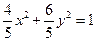 (2)略 (3)
(2)略 (3)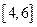
(1)由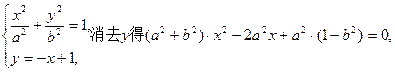
由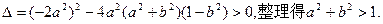
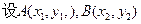 ,
,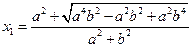 ,
,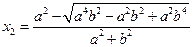
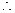
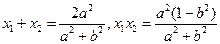 ,
,
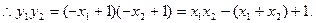
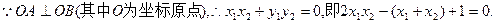
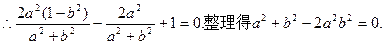
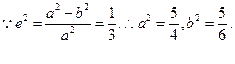 ,
,
(2)由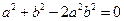 整理得
整理得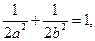
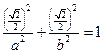 ,
,
则不论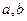 如何变化,椭圆恒过第一象限内的定点
如何变化,椭圆恒过第一象限内的定点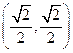
(3)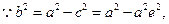 将(1)中的
将(1)中的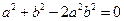
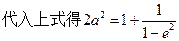 ,
,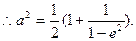
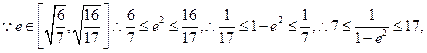
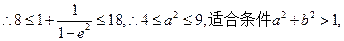 由此得
由此得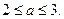
 即长轴长的范围为
即长轴长的范围为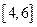
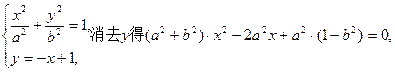
由
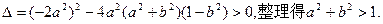
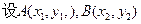 ,
,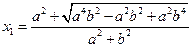 ,
,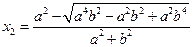
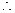
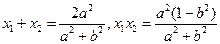 ,
,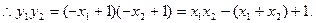
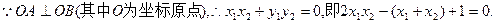
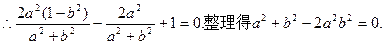
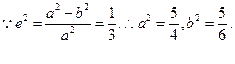 ,
,
(2)由
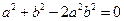 整理得
整理得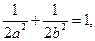
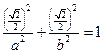 ,
,则不论
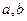 如何变化,椭圆恒过第一象限内的定点
如何变化,椭圆恒过第一象限内的定点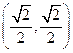
(3)
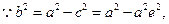 将(1)中的
将(1)中的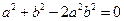
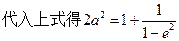 ,
,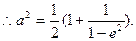
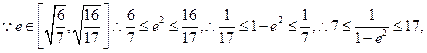
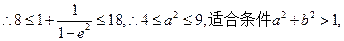 由此得
由此得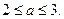
 即长轴长的范围为
即长轴长的范围为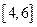

练习册系列答案
相关题目
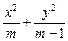 =1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D,设f(m)=||AB|-|CD||
=1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D,设f(m)=||AB|-|CD||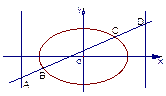
 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线 的距离分别为d1、d2,试求d1·d2的值,并判断直线L与椭圆M的位置关系。
的距离分别为d1、d2,试求d1·d2的值,并判断直线L与椭圆M的位置关系。 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线  (m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1·d2的值。
(m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1·d2的值。


 到焦点F2的距离也成等差数列。
到焦点F2的距离也成等差数列。
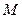 与椭圆
与椭圆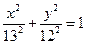 的左焦点和右焦点的距离之比为
的左焦点和右焦点的距离之比为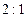 ,求点
,求点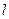 交椭圆
交椭圆 于
于 两点,椭圆与
两点,椭圆与 轴的正半轴交于
轴的正半轴交于 点,若
点,若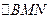 的重心恰好落在椭圆的右焦点,则直线
的重心恰好落在椭圆的右焦点,则直线



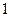 ,离心率
,离心率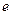 满足
满足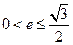 ,求长轴的最大值。
,求长轴的最大值。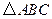 中,
中,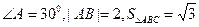 .若以
.若以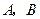 为焦点的椭圆经过点
为焦点的椭圆经过点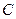 ,则该椭圆的离心率
,则该椭圆的离心率 .
.