题目内容
9.设函数f(x)=|x+$\frac{4}{a}$|+|x-a|(a>0).(1)证明:f(x)≥4;
(2)若f(3)<5,实数a的取值范围.
分析 (1)利用绝对值三角不等式,结合基本不等式,即可证明;
(2)若f(3)<5,即|3+$\frac{4}{a}$|+|3-a|<5,进而$\frac{4}{a}$-2<a-3<2-$\frac{4}{a}$,即可求出实数a的取值范围.
解答 (1)证明:f(x)=|x+$\frac{4}{a}$|+|x-a|≥|$\frac{4}{a}$+a|=|$\frac{4}{a}$|+|a|≥2$\sqrt{|\frac{4}{a}||a|}$=4;
(2)解:若f(3)<5,即|3+$\frac{4}{a}$|+|3-a|<5,
∵a>0,∴3+$\frac{4}{a}$+|3-a|<5,
∴|3-a|<2-$\frac{4}{a}$,
∴$\frac{4}{a}$-2<a-3<2-$\frac{4}{a}$,
∴1<a<4.
点评 本题考查绝对值三角不等式,基本不等式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
20.若A={(a,c)|1≤a≤2,0≤c≤1,a,c∈R},则任取(a,c)∈A,关于x的方程ax2+2x+c=0有实根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{ln2}{2}$ | C. | ln2 | D. | 1-ln2 |
14.若f(x)=$\frac{1}{2}$ax2+2x-lnx(a≠0)在区间[1,2]上是增函数,则实数a的最小值为( )
| A. | 1 | B. | -1 | C. | -$\frac{3}{4}$ | D. | -2 |
19.已知函数f(x)=$\sqrt{3}$sin2x-cos2x-2m在[0,$\frac{π}{2}$]上有两个零点,则m的取值范围为( )
| A. | [$\frac{1}{2}$,1) | B. | ($\frac{1}{2}$,1] | C. | [$\frac{\sqrt{3}}{2}$,1) | D. | ($\frac{\sqrt{3}}{2}$,1] |
 如图,60°的二面角棱上有A′,B′两点,直线AA′,BB′分别在这个二面角的半平面内,且都垂直于A′B′,已知A′B′=3,AA′=3,BB′=5,则AB的长度为2$\sqrt{7}$.
如图,60°的二面角棱上有A′,B′两点,直线AA′,BB′分别在这个二面角的半平面内,且都垂直于A′B′,已知A′B′=3,AA′=3,BB′=5,则AB的长度为2$\sqrt{7}$.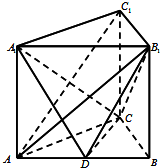 如图,三棱柱ABC-A1B1C1侧棱垂直于底面,AB=4,AC=BC=3,D为AB的中点.
如图,三棱柱ABC-A1B1C1侧棱垂直于底面,AB=4,AC=BC=3,D为AB的中点.