题目内容
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,上顶点为
,上顶点为![]() ,右焦点为
,右焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 为
为![]() 轴上的两个动点,且
轴上的两个动点,且![]() ,直线
,直线![]() 和
和![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求![]() 的面积最小值;
的面积最小值;
(ⅱ)证明:![]() 三点共线.
三点共线.
【答案】(Ⅰ)![]() ;
;
(Ⅱ)(ⅰ)2;
(ⅱ)证明过程见解析.
【解析】
(Ⅰ)根据离心率可以得到等式,由![]() 的面积为
的面积为![]() ,又得到一个等式,结合
,又得到一个等式,结合![]() ,可以求出
,可以求出![]() 的值,这样就求出椭圆方程;
的值,这样就求出椭圆方程;
(Ⅱ)(ⅰ)设出![]() 两点坐标,根据
两点坐标,根据![]() ,可以得到
,可以得到![]() 两点坐标之间的关系,求出
两点坐标之间的关系,求出![]() 的面积的表达式,利用基本不等式求出
的面积的表达式,利用基本不等式求出![]() 的面积最小值;
的面积最小值;
(ⅱ)直线![]() 的方程与椭圆方程联立,求出
的方程与椭圆方程联立,求出![]() 点坐标,同理求出
点坐标,同理求出![]() 的坐标,求出直线
的坐标,求出直线![]() 的斜率,根据
的斜率,根据![]() 两点坐标之间的关系,可以证明出直线
两点坐标之间的关系,可以证明出直线![]() 的斜率相等,又过同一点,这样就可以证明
的斜率相等,又过同一点,这样就可以证明![]() 三点共线.
三点共线.
(Ⅰ)由题意可知:![]() ,离心率为
,离心率为![]()
![]() ,
,
因为![]() 的面积为
的面积为![]() ,所以
,所以![]()
![]()
![]() 而
而![]() ,
,
所以![]() ,因此
,因此![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() ;
;
(Ⅱ)设![]() ,
,![]()
![]()
![]() ,所以
,所以![]() .
.
(ⅰ)设![]() 的面积为
的面积为![]() ,
,![]() ,
,
![]() ,当且仅当
,当且仅当![]() 时,取等号,所以
时,取等号,所以![]() 的面积最小值为2;
的面积最小值为2;
(ⅱ)![]() ,直线
,直线![]() 的方程为:
的方程为:![]() 与椭圆的方程联立得
与椭圆的方程联立得
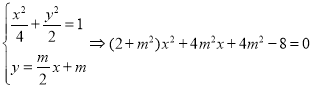 ,
,
设![]() 所以有
所以有![]() ,
,![]() ,
,
设![]() ,同理求出
,同理求出![]() ,所以
,所以![]() ,
,
![]() ,
,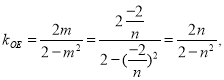 所以
所以![]() ,直线
,直线![]() 过同一点,斜率相等,所以
过同一点,斜率相等,所以![]() 三点共线.
三点共线.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目