题目内容
【题目】如图所示，正方体
的棱长为
， 
， 
分别是棱
， 
的中点，过直线
， 
的平面分别与棱
， 
交于
， 
，设
， 
，给出以下四个命题：
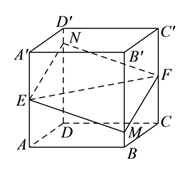
①四边形
为平行四边形；
②若四边形
面积
， 
，则
有最小值；
③若四棱锥
的体积
， 
，则
是常函数；
④若多面体
的体积
， 
，则
为单调函数．
其中假命题为（ ）．
A. ① B. ② C. ③ D. ④
【答案】D
【解析】对于①，∵平面
平面
，
∴
，
同理： 
，
∴四边形
为平行四边形，故①正确；
对于②，四边形
的面积
，
当
为
的中点时，即
时， 
最短，
此时面积最小，故②正确；
对于③，
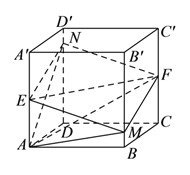
连接
， 
， 
，
则四棱锥分割为两个小棱锥，它们是以
为底，以
， 
为顶点的两个小棱锥，
因为
的面积是个常数， 
， 
到平面
的距离和是个常数，
所以四棱锥
的体积
是常函数，故③正确；
对于④，多面体
的体积
为常数函数，故④错误．
综上所述，假命题为④．
故选
．
练习册系列答案
相关题目
