Question

（2013•许昌二模）在平面直角坐标系xOy中，平面区域W中的点的坐标（x，y）满足x²+y²≤4，从区域W中随机取点M（x，y）．
（Ⅰ）若X∈Z，y∈Z，令ξ=x²+y²，求ξ=4的概率；
（Ⅱ）已知直线l：y=-x+b（b＞0）与圆x²+y²=4相交所截得的弦长为2

2

．求y≥-x+b的概率．

Answer 1

分析：（Ⅰ）列举可得总的基本事件，找出ξ=4时包含的基本事件，可得答案；
（Ⅱ）由已知可得平面区域W的面积是4π，作出图象，可得满足y≥-x+b的点M构成的区域面积为S=π-2，由几何概型的公式可得答案．

解答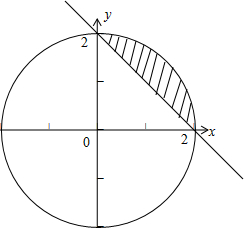：解：（Ⅰ）若X∈Z，y∈Z，则满足条件的点共有13个，
即（-2，0）（-1，0）（0，0）（1，0）（2，0）（-1，1）（0，1）
（1，1）（-1，-1）（0，-1）（1，-1）（0，2）（0，-2
ξ=4时，包含的基本事件有（-2，0）（2，0）（0，2）（0，-2）共4个，
故P（ξ=4）=

4

13

（Ⅱ）由已知可得平面区域W的面积是4π，
因为直线l：y=-x+b（b＞0）与圆x²+y²=4相交所截得的弦长为2

2

．如图
可得扇形的圆心角为

π

2

，
则满足y≥-x+b的点M构成的区域面积为S=π-2，（阴影）
所以y≥-x+b的概率为

π-2

4π

点评：本题考查古典概型和几何概型的计算，列举和数形结合是解决问题的关键，属基础题．