题目内容
已知函数 是偶函数,当
是偶函数,当 时,
时, 恒成立,设
恒成立,设 ,则
,则 的大小关系为( )
的大小关系为( )
A. B.
B. C.
C. D.
D.
【答案】
A
【解析】
试题分析:因为 时,
时, 恒成立,所以f(x)在
恒成立,所以f(x)在 上是增函数,又因为函数
上是增函数,又因为函数 是偶函数,所以函数f(x)关于直线x=2对称,所以f(x)在
是偶函数,所以函数f(x)关于直线x=2对称,所以f(x)在 上是减函数,因为
上是减函数,因为 ,所以f(6)>f(-1)>f(3),即b<a<c.
,所以f(6)>f(-1)>f(3),即b<a<c.
考点: 抽象函数的单调性与奇偶性,利用其比较数的大小.
点评:由 时,
时, 恒成立, 确定f(x)在
恒成立, 确定f(x)在 上是增函数是解题的关键,然后再根据函数
上是增函数是解题的关键,然后再根据函数 是偶函数,所以函数f(x)关于直线x=2对称,f(x)在
是偶函数,所以函数f(x)关于直线x=2对称,f(x)在 上是减函数,从而转化自变量与对称轴x=2的距离大小的比较问题.
上是减函数,从而转化自变量与对称轴x=2的距离大小的比较问题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 是偶函数,且
是偶函数,且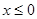 时,
时,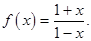 。
。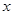 >0时
>0时 ,证明:
,证明:
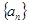 的首项
的首项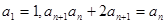 。
。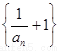 是等比数列,并求
是等比数列,并求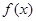 是偶函数,且对任意
是偶函数,且对任意 均有
均有 ,当
,当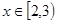 时,
时,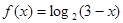 ,求使
,求使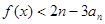 恒成立的
恒成立的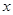 的取值范围。
的取值范围。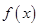 是偶函数,且
是偶函数,且 时,
时, .求
.求 的值,
的值, 时
时 的值;
的值;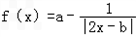 是偶函数,a为实常数.
是偶函数,a为实常数. 的首项
的首项 。
。 是等比数列,并求
是等比数列,并求 是偶函数,且对任意
是偶函数,且对任意 均有
均有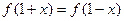 ,当
,当 时,
时,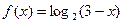 ,求使
,求使 恒成立的
恒成立的 的取值范围。
的取值范围。