题目内容
已知函数 是偶函数,且
是偶函数,且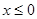 时,
时,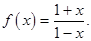 。
。
(1)求当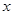 >0时
>0时 的解析式; (2) 设
的解析式; (2) 设 ,证明:
,证明:
【答案】
(1) 时,
时, 的解析式为:
的解析式为:
(2) 的解析式为:
的解析式为: ,见解析。
,见解析。
【解析】
试题分析:(1)设 (1分),因为
(1分),因为 时,
时, ,所以
,所以
 (3分) 又因为函数
(3分) 又因为函数 是偶函数,所以
是偶函数,所以 (4分)
(4分)
故 时,
时, 的解析式为:
的解析式为: (6分)
(6分)
(2)由(1)知: 的解析式为:
的解析式为: (7分)
(7分)
① 时,因为
时,因为 ,(8分)
,(8分) 
 (9分)
(9分)
所以 (10分)同理可证:②
(10分)同理可证:②  ,
, (11分)
(11分)
综上所述: 时,
时, (12分)
(12分)
考点:本题考查偶函数定义、函数值的求法、分类讨论思想。

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 是偶函数,且
是偶函数,且 ,当
,当 时,
时, ,则方程
,则方程 在区间
在区间 上的解的个数是( )
上的解的个数是( ) 是偶函数,且
是偶函数,且 则
则 ( )
( ) B.
B.
 C.
C.
 D.
D.

 是偶函数,且
是偶函数,且 则
则 ( )
( ) B.
B.
 C.
C.
 D.
D.

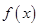 是偶函数,且
是偶函数,且 时,
时, .求
.求 的值,
的值, 时
时 的值;
的值; 的首项
的首项 。
。 是等比数列,并求
是等比数列,并求 是偶函数,且对任意
是偶函数,且对任意 均有
均有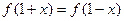 ,当
,当 时,
时,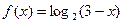 ,求使
,求使 恒成立的
恒成立的 的取值范围。
的取值范围。